- Mise En Oeuvre
- L’implémentation
- Matériel et langage
- Matériel
- Langage
Maintenant que nous avons vu les principales étapes nécessaires à la reconstruction, nous allons pouvoir les implémenter.
Si l’utilisation d’une méthode directe pour la résolution a été envisagée, cela vient certainement du fait que le centre CYCERON possède un supercalculateur qui autorise le calcul sur des volumes de données importants.
Le Centre CYCERON dispose d’un supercalculateur CRAY J916 appartenant à la série des J90. Ce système possède l’architecture vectorielle des systèmes CRAY. Il comporte aujourd’hui 4 modules de 4 processeurs. Le J916 est typiquement une machine à mémoire partagée.
Le CRAY est intégré au réseau VIKMAN et peut ainsi être utilisé en tant que serveur de calcul. Son interface FDDI garantit une grande vitesse d’accès au réseau.
La période d’horloge est de 10 ns (100mhz). Grâce à l’architecture vectorielle, la puissance en crête atteint 200 MegaFlops (nombres d’opérations sur des réels flottants par seconde), soit une puissance en crête de 3.2 GigaFlops pour le système complet. (Une station Silicon Graphics peut atteindre 40 MegaFlops).
La plupart des problèmes nécessitant l’emploi d’un supercalculateur traitent d’un volume de données important et font de nombreux accès à la mémoire. L’efficacité ne dépend pas alors que de la rapidité de calcul proprement dite mais aussi de la bande passante de la mémoire. Pour le Cray J916, tous les processeurs peuvent accéder à n’importe quel mot de la mémoire. Même s’il existe des limitations au accès mémoire, le débit maximal, la bande passante, est de 32 mots mémoires par période d’horloge.
Les différents programmes sont implémentés en Fortran90. Ce langage est particulièrement adapté dans le domaine du calcul. Cette version est beaucoup plus souple que celle du Fortran77. Il s’agit d’un langage de programmation structurée, avec des possibilités de programmation modulaire et d’allocations dynamiques.
L’atout principal de ce langage tient dans la manipulation des tableaux et des matrices où :
- Les opérations entre matrices s’écrivent de manière quasi directe.
- Des portions de tableau sont facilement exploitables.
- Des fonctions intrinsèques sont déjà implémentées.
Mais une reconstruction n’est rien dans l’absolu, il nous faut des données à reconstruire et ensuite nous avons besoin d’outils pour valider la reconstruction.
- Pour les données
A ce niveau, au bout du compte, on souhaite disposer d’un Sinogramme. Le sinogramme est un tableau bidimensionnel dont l’ordonnée donne la direction de projection et l’abscisse un capteur de la barrette placée perpendiculairement à cette direction. A chaque couple (Direction, Capteur) est associée une valeur représentant le nombre de coups pour ce capteur. Dans la pratique, c’est sous cette forme que sont obtenus les résultats de mesure à l’issue d’un examen TEP.
Les Sinogrammes que nous utilisons sont principalement de deux sortes :
Pour ces sinogrammes, on choisit une image représentative de notre fantôme. On se fixe un modèle de projection (comme nous l’avons au chapitre) et, en accord avec ce dernier, on projette l’image. Les résultats sont stockés sous la forme du tableau bidimensionnel désiré.
Les sinogrammes sont donc issus :
- D’une projection par bande où l’image est parcourue Pixel par Pixel.
- D’une projection par bande avec des incréments du dixième du pixel (Decipixel).
- D’une projection interpolée.
- D’une simulation de Monte Carlo. [RB7]
Dans les 3 premiers cas, les sinogrammes obtenus sont exempts de bruit de nature physique. Seuls subsistent des erreurs liées à la discrétisation. C’est pourquoi un générateur de bruit a été implémenté. On peut donc bruiter le sinogramme de manière additive par un bruit uniforme ou gaussien mais aussi réaliser à partir d’un sinogramme un tirage suivant une loi de Poisson. Dans le premier cas, l’amplitude ou la variance du bruit est modulable. Dans le deuxième cas, pour chaque pixel dont l’activité est x, on réalise un tirage selon une loi de Poisson d’espérance x.
Par sinogrammes mesurés, on sous-entend tous les sinogrammes que fournissent les caméras TEP. Ce sont des données réelles issues d’examens.
Ces sinogrammes représentent l’information dont on dispose. Si on fixe un ordre de lecture du tableau bidimensionnel, on obtient cette information sous la forme d’un vecteur p : point de départ de la résolution de notre système p=Hc.
La reconstruction va reprendre les éléments que nous avons décrits dans les chapitres précédents. Résumons-en l’essentiel :
Pour élaborer notre système p=Hc nous avons dû :
- Faire le choix d’un mode de projection en accord avec la géométrie et la physique de l’acquisition pour le remplissage de H.
- Faire le choix d’un base de reconstruction de l’image (c)
- Poser l’hypothèse d’un lien linéaire
Nous avons également choisi de réaliser l’inversion directe du système obtenue par l’utilisation d’une factorisation soit SVD soit QR Householder.
Ces éléments, comme p est issu des sinogrammes, guident naturellement vers l’implémentation de la reconstruction
- Saisie des différentes données
- Construction de H
- Résolution par inversion. A l’aide de p et H on estime le vecteur c.
- Reconstruction de l’image
On retrouve ces différentes étapes plus en détail sur la figure 4 de la table des illustrations.
Maintenant que la reconstruction est effectuée, on va chercher à en estimer la qualité.
- Pour les Tests
- Rms Distance[RB8] [RB13]
- Moments
Dans le cas où les images reconstruites ont été obtenues à partir de sinogrammes calculés, on connaît l’image exacte. Ainsi pour réaliser une évaluation quantitative, ou plus précisément pour mesurer l’écart de l’image reconstruite avec l’image originale, nous calculerons un écart quadratique moyen relatif ( Root Mean Square distance ) :
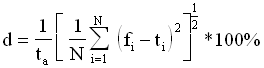
où :
fi représente la valeur du pixel i sur l’image reconstruite
ti représente la valeur du pixel i sur l’image originale
N le nombre de pixels considérés
ta la valeur moyenne sur cet ensemble de pixels
Cette distance peut être calculée sur la totalité ou seulement sur une partie de l’image suivant les besoins.
Si, sur l’image originale, on sait qu’une certaine zone est uniforme, on va chercher à caractériser comment les pixels de l’image reconstruite s’organisent dans cette zone.
Cette caractérisation va passer par le calcul de la moyenne des pixels f1,.....,fN:
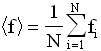
qui estime la valeur centrale sur la zone autour de laquelle oscillent les pixels.
Il est nécessaire également, connaissant la valeur centrale, de savoir quelle est l’amplitude des variations autour de cette valeur. On le fait en recherchant la variance sur la zone :

ou la déviation standard :
![]()
Un autre estimateur possible est la déviation moyenne absolue :
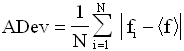
Bien qu’implémentés, les moments d’ordre 3 et 4, skewness et kurtosis seront laissés de coté.
- Résultats et discussion
- Fantômes utilisés pour les sinogrammes calculés
- disque
- fant1
- irm
- Premières reconstructions et premières constatations
- Illustration
- Factorisation SVD ou QR
- Temps de calcul
- Espace mémoire
- Reconstruction et géométrie d’acquisition
- Influence du nombre de capteurs
- Nombres moyens de données par éléments de la base
- Reconstruction et information a priori
- Ajuster une surface et non un plan.
- Taille de l'information a priori
Sur une image de dimension 128*128 pixels, on considère un disque uniforme d’un rayon de 50 pixels centré sur l’image. Ce disque correspond à une zone d’activité constante dont l’intensité variera et sera précisée au cours des expériences.
Le fantôme fant1.128 correspond à une image 128*128 sur laquelle une région elliptique décentrée représente une activité de fond. L’intensité sur cette région est de 5. Deux ouvertures rectangulaires ont été mises à zéro à l’intérieur de cette zone. Les deux régions circulaires haut à gauche et la région elliptique en bas représentent des zones chaudes d’intensités respectives 5, 7.5 et 11.
Ce fantôme irm.128 est réalisé à partir d’une image irm de dimension 128*128 segmentée substance blanche/substance grise, sur laquelle on a ajouté 2 points chauds. L’intensité de la substance grise va être de 1, celle de la substance blanche de 4. Les points chauds sont, un disque de rayon 5 pixels d’intensité 14, et un de rayon 2 pixels d’intensité 7.
Les deux derniers fantômes sont représentés dans la table des illustrations Figure 5 et 6.
A titre d’exemple, pour la reconstruction directe, nous allons projeter le disque de différentes manières. La valeur moyenne sur ce disque est alors de 4.82 dans le cas d’une projection par bande et de 2.16 dans le deuxième cas. Pour notre sinogramme, nous projetons suivant 222 directions avec des barrettes de 64 capteurs d’une largeur de 2 pixels. Après reconstruction, les images auront une résolution de 128*128 pixels.
Les résultats sont représentés figure 7 de la table des illustrations.
Le fait de pouvoir choisir une base de reconstruction, un mode de projection, une méthode de projection fournit un grand nombre de combinaisons possibles. Dans l’exemple précédent, on cherchait juste à donner une idée de la reconstruction pour différentes bases de reconstruction. C’est pourquoi seule la reconstruction utilisant une factorisation QR a été envisagée et le mode de remplissage de H était limité au cas le plus simple d’une projection par bande en parcourant l’image pixel par pixel. Nous allons par la suite, chercher à montrer parmi les nombreuses combinaisons quelles sont celles ayant un sens et un intérêt pratique.
Nous avons, dans l’illustration précédente, uniquement utilisé une factorisation QR... Pourquoi ?
Nous avons vu dans le chapitre précédent, qu’à l’aide d’une factorisation QR Householder avec permutation des colonnes, on pouvait trouver une solution au sens des moindres carrés de notre système. Cette solution n’était pas une solution de norme minimale mais s’en approchait. La factorisation SVD permettait également de trouver une solution, cette fois-ci de norme minimale. Dans les deux cas, une certaine régularisation du problème était possible. Alors entre SVD et QR, laquelle choisir ?
Une première remarque, qui ne nous aidera pas dans notre choix, est que les reconstructions obtenues par l’une ou l’autre de ces deux factorisations, sont d’aussi bonne qualité.
On va donc privilégier la méthode présentant le temps de calcul et l’encombrement mémoire les plus faibles.
A partir d’un sinogramme de 222 directions avec des barrettes de 64 capteurs d’une largeur de 2 pixels, reconstruisons, pour chacune des deux méthodes, une image sur une base de pavés(= base de pixels de décomposition de résolution n*n pixels de représentation). Pour celle-ci, H est calculé en accord avec une projection suivant des bandes.
Dans le cas d’une reconstruction par SVD, le temps global comprenant les saisies et le chargement des images est de 208 secondes, le temps net de calcul est alors de 206 secondes. Dans le cas d’une reconstruction QR, ces temps sont respectivement de 90 secondes et 52 secondes. Ce gain de 4 entre les deux temps de reconstructions est loin d’être un facteur négligeable. Ce gain provient principalement du fait que la factorisation SVD n’est pas parallélisée et donc n’est effectuée que sur un processeur. La factorisation QR, elle, est parallélisée s’effectue donc sur les 16 processeurs du CRAY. Dans notre problème des moindres carrés, la matrice H a plus de lignes que de colonnes. Pour gagner du temps, lors de la factorisation SVD, on calcule donc le produit HTH puisque cette matrice est plus petite que H. Cependant ce produit, bien que parallélisé, prend du temps.
Une reconstruction sur une base de 64*64 paves prend 608 secondes à l’aide d’une factorisation QR. On est loin des 3 secondes que prend la rétroprojection filtrée.
La matrice H étant en général de grande taille, cela pose rapidement des problèmes : 222 directions de projections, 64 barrettes de capteurs, une base de 32*32 pixels, cela représente une matrice H de 14208 lignes et de 1024 colonnes, soit pas moins de 14.5 millions d’éléments. On atteint vite les capacités limites de la machine quand on augmente la dimension de la base de reconstruction.
Pour la SVD, Le calcul de HTH, du moins comme il a été implémenté, suppose la présence simultanée de HT et H. De plus, lors de la décomposition SVD de HTH, on doit mémoriser les matrices U, L , et V. Heureusement le calcul de HTH produit une matrice carrée de taille utile fortement inférieure à celle du nombre d’éléments de la base. En effet, H a des colonnes qui sont nulles. Pour une résolution par SVD l’encombrement mémoire est donc d’un peu plus de 2 fois H.
Dans le cas de la reconstruction QR, on s’est affranchi du produit HTH et lors de la factorisation, la matrice Q n’est pas calculée explicitement. Seuls les vecteurs v sont conservés (voir chapitre précédent) et du fait des zéros qui apparaissent sous la diagonale lors de la factorisation, ces vecteurs peuvent être directement mémorisés dans la matrice H. La reconstruction par une factorisation QR nécessite donc un peu plus de H en place mémoire. Ce gain de 2 n’est pas non plus négligeable.
Pour les deux raisons précédentes, dans le cas d’une solution au sens des moindres carrés , on préférera donc la factorisation QR Householder avec permutation des colonnes..
Dans les reconstructions qui suivront, on n’envisagera, sauf mention particulière, que ce type de résolution. De plus pour limiter le nombre de possibilités, on n’envisage le remplissage de H qu’en accord avec un protocole de projection par bande et nous nous limitons à une base de pavés.
Pour l'image fant1.128, on va calculer les sinogrammes en conservant un nombre de projections constant (212 directions), mais en faisant varier le nombre de capteurs sur une barrette. On s'arrange pour que la totalité de l'image soit vue en permanence. A l ’aide de ces sinogrammes et pour un pavage constant, on va reconstruire successivement les images. Le fantôme original est injecté comme information à priori et le calcul de la Rms distance est effectué sur toute l'image. On obtient alors les résultats suivants :
|
|
16.00 |
32.00 |
64.00 |
128.00 |
|
|
8.00 |
4.00 |
2.00 |
1.00 |
|
Rms dist. 16 Pavés |
4.07 |
1.23 |
0.93 |
0.89 |
|
Rms dist. 32 Pavés |
6277 |
9.14 |
2.89 |
2.68 |
|
Rms dist. 48 Pavés |
66.51 |
23.24 |
6.28 |
5.07 |
Si maintenant, on reconstruit sans fournir d'information a priori et que pour le calcul de la Rms distance on ajuste la résolution de l'image source au pavage de la reconstruction, on obtient les résultats suivants :
|
NbCapteurs |
16.00 |
32.00 |
64.00 |
128.00 |
|
Nb Pixels |
8.00 |
4.00 |
2.00 |
1.00 |
|
Rms dist. 16 Pavés |
52.11 |
17.09 |
14.58 |
12.99 |
|
Rms dist. 32 Pavés |
337.21 |
37.44 |
12.69 |
9.65 |
|
Rms dist. 48 Pavés |
165.70 |
61.52 |
15.58 |
10.17 |
Même si les distances mentionnées dans ce tableau ne peuvent être appréhendées dans l'absolu, on peut en dégager une tendance générale. On voit que pour une base de dimension fixée (NbPavés), la distance après reconstruction diminue à mesure que le nombre de capteurs augmente jusqu'à ce que ce nombre soit supérieur à la résolution. La distance devient alors constante.
Cette constatation est importante et il est nécessaire de s’y arrêter plus longuement. Pour cela, on va considérer le fantômes irm.128. On va réaliser une série de sinogrammes utilisant le modèle de projection par bande, en faisant varier le nombre de directions, et le nombre de capteurs. Dans chaque cas, les sinogrammes seront bruités suivant un modèle de bruit poissonien.
Le tableau suivant regroupe les caractéristiques du sinogramme, la rms distance calculée vis à vis de l’image originale et les valeurs extrêmes obtenues après reconstruction sur une base de 32*32 (ou de 64*64 pavés). La rms distance est calculée seulement sur une masque elliptique englobant la zone active et en référence à l’image originale ajustée à la résolution de 32*32 (ou de 64*64 pavés)
|
Sinogrammes |
NbCapteurs |
32(4pixels) |
64(2pixels) |
128 |
||||
|
|
Nb Directions |
100 |
500 |
1000 |
40 |
250 |
150 |
|
|
|
NbPavés |
32(4pixels) |
32 |
32 |
64 |
64 |
||
|
Reconstruction |
Rms distance |
353.7 |
188.6 |
130.9 |
50.3 |
24.6 |
140.3 |
29.9 |
|
|
Minimum |
-23.6 |
-18.15 |
-7.58 |
-3.31 |
-0.67 |
-9.37 |
-1.58 |
|
|
Maximum |
28.13 |
24.14 |
13.47 |
12.24 |
11.56 |
20.01 |
16.38 |
|
Figure |
Figure 9 |
Figure 10 |
||||||
|
|
1 |
2 |
3 |
4 |
5 |
1 |
2 |
|
Dans le cas de la reconstruction de l’image à partir du sinogrammes à 128 capteurs, la rms distance vis à vis de l’image originale (si cette dernière n’est pas ajustée au pavage de 64*64) est de 76.5. A titre de comparaison, la rms distance obtenue par une rétroprojection filtrée est de 64.37.
Le tableau ci dessus est assez explicite. Lorsque le nombre de pixels par pavés de reconstruction est inférieur, à la limite égal, au nombre de pixels que voit un capteur (image 1,2,3), le système malgré un nombre de données toujours croissant (jusqu’à 1000 directions) aura du mal à retrouver l’image initiale.
Ce problème n’est donc pas lié à un nombre de redondances insuffisant et se manifeste, quelle que soit la base de reconstruction, dès que l’on cherche à reconstruire une image avec une résolution (au sens de la représentation) inférieure à celle que voit le capteur.
C’est une limitation forte de notre système, qui vient certainement d’une violation du théorème d’échantillonnage dans ce cas là. Il s’avère alors nécessaire de penser différemment la géométrie d’acquisition. [RB11]
Par la suite, on suppose que les différentes reconstructions sont en accord avec cette règle :
Résolution de l’image reconstruite < Résolution des Capteurs
Pour une base de pavés, cette condition équivaut à :
Cette règle étant posée, on peut maintenant chercher à savoir comment la reconstruction de sinogrammes bruités va évoluer en fonction du nombre de données disponibles.
Pour un fantôme, on va réaliser une série de sinogrammes, pour lesquels varie le nombre de directions. Le nombre de capteurs d’une largeur de 2 pixels est fixé à 64 . Chacun de ces sinogrammes, calculés par une projection par bande, va ensuite être bruité par un bruit additif gaussien dont la variance sera successivement 2,5,9,14,20% du nombre de coups maximum sur le sinogramme. On va reconstruire les images sur une base de pavés dont le nombre d’éléments sera successivement 162, 242, 322, 402, 482, 562 . Lors de la reconstruction, on injecte comme information à priori le fantôme lui même. On calcule ensuite la rms distance, la moyenne et la variance sur la zone uniforme de ce fantôme par rapport à l’image originale. On va s’intéresser plus particulièrement aux critères de rms distance et de variance en fonction du nombre moyen de données. Par nombre moyen de données on comprend le rapport du nombres de données de projections (Nbdirection*NbCapteurs) sur le nombre d’éléments de la base (NbPavés2).
On obtient pour le fantôme fant1 :

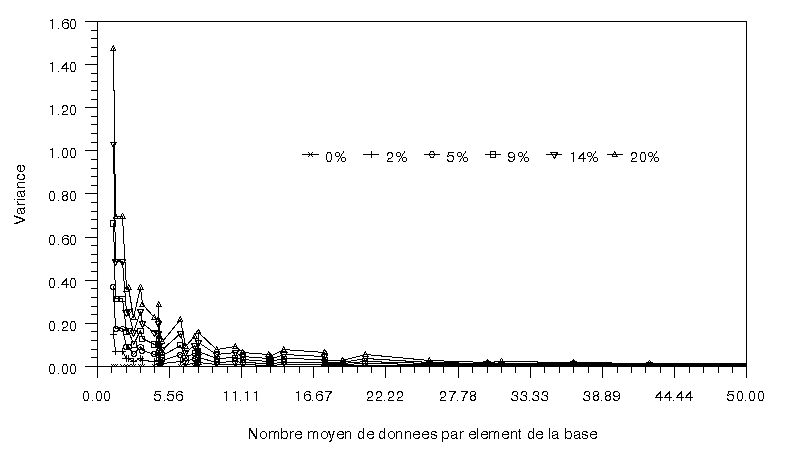
et pour le fantôme disque uniforme où l’intensité est de 4.82.

Ce critère nombre moyen de données permet donc de traduire les redondances du système. Si ce nombre est assez élevé, la reconstruction même bruitée sera assez proche de l’image originale.
Pour une distance à l’image originale fixée, on peut ainsi connaître, à partir d’une telle courbe, le nombre de données, ie le nombre de projections et de capteurs requis.
Dans le cas d’une résolution sur une base de pavés, on a déjà vu précédemment que le pavage ne pouvait être choisi de manière quelconque et qu'il était étroitement lié au nombre de capteurs dont on dispose lors de la mesure. (paragraphe 1.2.3.1).
Dans le cas où la base de pavés n’est pas contrainte par une matrice d’information a priori, la résolution de l’image reconstruite est celle du nombre de pavés. Il semble normal alors qu’en augmentant le pavage, l'image reconstruite va se rapprocher de l'image originale qui est de résolution 128*128.
Mais une autre constatation s'impose...
Pour cela, à l'aide du sinogramme issu du fantôme fant1.128 projeté suivant 200 directions sur des barrettes de 60 capteurs de 4 pixels, on va reconstruire des images en augmentant régulièrement le nombre de pavés. La matrice H est conditionnée par l'information a priori exacte fant1.128. On va s'intéresser alors à la distance quadratique moyenne ainsi qu'aux propriétés statistiques sur une partie uniforme de l'image fant1.128.masque.
les résultats obtenus sont les suivants :
|
NB Pavés |
16 |
20 |
24 |
28 |
32 |
48 |
|
Rms Dist. |
0.53 |
0.95 |
1.43 |
1.71 |
2.42 |
4.88 |
|
Moyenne |
4.95 |
4.95 |
4.95 |
4.95 |
4.95 |
4.95 |
|
Variance |
0.172 |
0.175 |
0.175 |
0.180 |
0.184 |
0.232 |
On s'aperçoit que lorsque le nombre de pavés augmente, la Rms distance mais également la variance sur une zone homogène de l'image augmente. En extrapolant on serait tenté de déduire que la reconstruction est meilleure dans le cas où le pavage est unitaire!!! C'est effectivement le cas...
Lors de la reconstruction conditionnée par de l’information a priori, on cherche, sur chaque pavé, le coefficient par lequel il est nécessaire de multiplier cette portion de surface injectée en information pour la faire coller le mieux qui soit en moyenne à la portion de surface correspondante de l'image originale
De fait, si l'information a priori est exacte (si la surface injectée en information a priori est identique en forme et en intensité à l'image à reconstruire), le fractionnement de cette image pour ajuster chaque partie induit, de par ce découpage, plus d'erreurs que si l'on cherchait à ajuster l'image a priori dans son ensemble. Ajuster l’image dans son ensemble consiste simplement à affecter le coefficient 1 à cette image.
Le découpage de l'image en pavés se justifie dans la pratique par le fait qu’on ne connaît évidemment pas exactement l'image à reconstruire. Autrement dit, on ne peut pas limiter la base de décomposition (les portions de surface) à un seul vecteur (une seule image ou un seul pavé), et on est obligé d'augmenter la dimension de l'espace de reconstruction (Nb de Pavés) pour que la décomposition sur cette base fournisse une bonne estimation de l'image originale.
Supposons maintenant que les images projetées soient des images de taille 256*256 et que les images reconstruites soient de taille 128*128. L'image 128*128, qui représentera lors de la reconstruction l'image exacte; est issue de l'image originelle 256*256 par un zoom. Ce zoom nécessite de faire une interpolation qui peut être :
- Relative au plus proche voisin
- Bilinéaire
- Bicubique
Cette interpolation va déjà induire une erreur supplémentaire lors de la reconstruction.
Pour le voir prenons le cas du fantôme fant1.256 qui va donner trois images de dimension 128*128
- fant1i1.128 interpolée au sens du plus proche voisin
- fant1i2.128 interpolée de manière bilinéaire
- fant1i3.128 interpolée de manière bicubique
Le fantôme fant1.256 est ensuite projeté suivant 200 directions. Chaque direction comporte 60 Capteurs de 4 pixels.
On reconstruit en utilisant une factorisation QR pour un pavage de 32*32 en injectant comme information à priori successivement chacune des trois images 128*128 obtenues précédemment. On trouve pour la rms distance par rapport à toute l’image originale :
- Rms Dist 1 12.15
- Rms Dist 2 2.89
- Rms Dist 3 2.92
Dans cet exemple, les images fant1i1, fant1i2, fant1i3 peuvent être considérées comme une information a priori exacte pour le fantômes fant1, et pourtant les reconstructions sont différentes.
Nous avions déjà pu constater visuellement ce phénomène lorsque nous avions illustré la reconstruction (paragraphe 1.2.2), puisque les images reconstruites associées à des projections voisines présentaient de légères différences. Les reconstructions sont donc sensibles à de petites perturbations. Dans l’exemple qui précède (où dans l’illustration au paragraphe 1.2.2.1), les modifications, entraînées par un désaccord entre la projection et le conditionnement de H, même si elles existent et sont visibles, n’affectent la solution que dans une proportion " raisonnable ". Il resterait à qualifier ce terme raisonnable et à s’assurer que de petites modifications n'entraînent pas de grands effets. Ne soyons pas trop défaitistes, le système semble ne pas trop mal se comporter du fait des différentes régularisations possibles.
Une question importante relative à la méthode de reconstruction reste le rôle de l'information a priori dans la reconstruction. Dans ce qui suit nous allons chercher à reconstruire le fantôme fant1i2.128 à l'aide d'un sinogramme ayant 200 directions de projections sur des barrettes de 60 capteurs. Lors de la reconstruction nous allons tout d'abord injecter les images iap1 puis iap2. (Table des illustrations Figure 11) Ces images n'ont rien à voir avec l'image à reconstruire mais présentent les particularités suivantes :
- Elles sont ajustées au pavage de reconstruction
- Elles ne comportent aucun pavé de valeur nulle
Après reconstruction on obtient deux images dont la Rms distance entre elles est de 0.0062. Cela revient à dire que les images sont quasi-identiques... Il n'y a derrière cela aucun tour de passe passe... Dans les images iap1, iap2 telles qu'elles sont décrites précédemment, nous avons sur chaque pavé une valeur constante. Pour un pavé donné, les valeurs sont différentes entre les deux images mais l'information contenue par pavé est la même.
Supposons que sur un pavé la valeur moyenne soit 1 sur iap1 et 2 sur iap2. Si sur l’image originale, on doit trouver 4 sur le pavé correspondant, le coefficient affecté lors de la résolution sera 4 pour l’image iap1 et 2 pour iap2. finalement le résultat sera le même. Dans les reconstructions précédentes, les bases de reconstruction s'avèrent analogues et toutes les images ajustées au pavage de reconstruction (en l'absence de pavés nuls) conduisent au même résultat.
L'information a priori ne prend son sens que si on introduit des variations au sein d'un pavé.
Les amplitudes sur cette portion de surface seront amplifiées par le coefficient résultant lors de l'inversion.
On peut en revanche se demander quel est le rôle des zéros introduits dans l'information a priori. Reprenons l'exemple précédent et construisons une image ajustée au pavage 32*32, n'ayant également aucun lien avec l'image à reconstruire. Ensuite on va mettre à zéro tous les pavés sur lequel on est sûr que la reconstruction ne doit rien donner. On obtient l’image iap3.
Lorsqu'on reconstruit en injectant une telle image, les résultats ne sont pas très différents de ceux obtenus précédemment. Mais alors quelle est l'influence de ces pavés mis à zéro?..
En introduisant des pavés nuls, on diminue la dimension de l'espace de reconstruction en limitant la base de décomposition.
Précédemment, lors de la reconstruction, les pavés que nous avons mis à zéro étaient affectés d'un petit coefficient. Ici, dès le départ, les vecteurs que représentent ces pavés sont supprimés de l'espace de reconstruction. On travaille sur un sous espace de dimension (Nbpaves2 - NbPavesNul) de l'espace de dimension Nbpaves2.
Dans la réalité, l’image à reconstruire nous est inconnue, on peut donc seulement injecter au niveau de la reconstruction une information A PRIORI, c’est à dire une hypothèse. Cette hypothèse, ne serait ce que par la nature aléatoire du bruit, sera toujours une version plus ou moins proche de la réalité. La question se pose alors de savoir comment se comporte le système lorsque le conditionnement se fait avec une version approchée de l’image à reconstruire.
Nous avons déjà mis en évidence précédemment que parler d’information a priori exacte restait ambigu (paragraphe 1.2.4.1.2). Pour notre information a priori approchée, on va cependant effectuer des modifications plus importantes sur la matrice de conditionnement. Pour le fantôme fant1, par exemple, on va faire disparaître les points chauds, pour ne conserver que l’activité de fond. On va également agrandir ou faire pivoter cette information a priori.
Les résultats obtenus sont alors représentés Figure 12 de la table des illustrations .
De ces résultats, on va extraire quelques profils qui vont mettre en évidence un point important de la reconstruction conditionnée par de l’information a priori. (Figure 13 de la table des illustrations)
Lors de la reconstruction qui utilise une information a priori réduite, et donc trop petite par rapport à l’image à reconstruire. il est nécessaire de remarquer que toute l’information qui normalement se retrouve à l’extérieur de ce cadre rigide, va se retrouver sur les bords de notre image reconstruite.
Lors de la reconstruction, on cherche une solution à notre problème pour la base choisie. La matrice de conditionnement, nous l’avons vu, génère une nouvelle base et les zéros introduits sur des pavés suppriment purement et simplement des éléments de la base. Dans le cas d’un information trop petite, la résolution va essayer sur cette base trop petite de trouver une solution proche de notre image réelle. Intuitivement on sent bien que mettre sur les bords l’information en trop par rapport à la base correspond bien à prendre une solution proche de la solution réelle.
Le même phénomène, plus général, s’observe lorsqu’on injecte comme information a priori, une information a priori pivotée par rapport à l’image réelle. Si on superpose la matrice de contrainte et l’image réelle à reconstruire, alors apparaissent des surplus et des manques entre ces deux images. Les surplus reviennent à supposer qu’à un endroit se trouve de l’information, alors qu’effectivement il n’y en pas, les manques reviennent à considérer une zone de reconstruction trop petite.
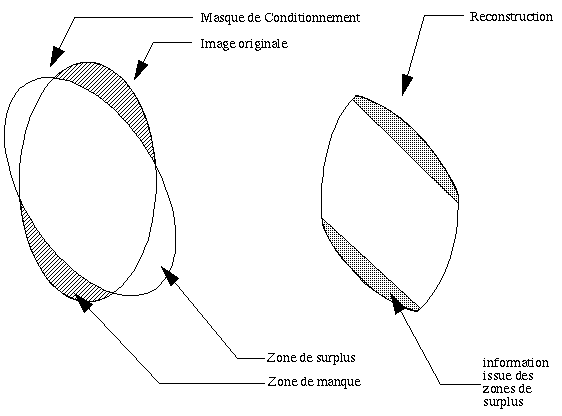
Les régions de surplus sont en général bien gérées lors de la reconstruction. Heureusement d’ailleurs, car c’est exactement ce que l’on fait quand on reconstruit sans information a priori. Cela revient à affecter une valeur constante sur toute l’image.
Un surplus correspond donc à considérer une base de reconstruction de dimension trop grande par rapport à celle de l’image à reconstruire. Ce n’est pas réellement gênant puisque l’espace de l’image réelle est contenu dans cet espace.
Afin d’effectuer une reconstruction proche de l’image originale, les régions de manque, comme précédemment dans le cas d’une information trop petite, vont être affectées des fortes valeurs lors de la reconstruction. Ce comportement de la résolution est assez ennuyeux. En effet, lors d’un examen, du fait du bruit, il se peut qu’une zone particulière de l’image normalement inactive contribue à la projection.
Si, en contraignant la résolution par un masque d’information à priori, une zone active est supprimée de la base de reconstruction, les valeurs de cette zone se retrouveront sur la reconstruction sous forme de hautes valeurs sur les bords de l’image reconstruite.
Pour conclure, il semble donc assez difficile de conditionner la reconstruction avec de l’information a priori. Puisque la rendre assez douce peut ne s’avérer d’aucune utilité (paragraphe 1.2.4.1.3) et qu’une information précise peut créer de fortes valeurs indésirées.
