Par le terme Projection, on désigne de manière générale, le lien physique existant entre l'activité radioactive et le jeu de données issues de la caméra. Modéliser ce lien physique n'est pas trivial...
Les photons issus de l'annihilation électron-positon sont détectés en coïncidence temporelle. Si on considère que les photons sont émis en opposition, on en déduit une ligne sur laquelle le positon avant annihilation était supposé se trouver.
Cette hypothèse de bon sens se modélise fort bien d'un point de vue mathématique. Dans un repère [Ox, Oy], on recueille dans une direction tout ce qui se trouve sur la ligne de coïncidence :


où ![]() représente la
projection suivant une droite de l'objet original O(x,y). La sommation
sur une droite passe par l'utilisation des distributions et plus
précisément par la distribution de Dirac d .
représente la
projection suivant une droite de l'objet original O(x,y). La sommation
sur une droite passe par l'utilisation des distributions et plus
précisément par la distribution de Dirac d .
Remarque :
Radon a pu montrer (1917) qu'il était possible de remonter à l'information bidimensionnelle à l'aide de ces projections (données mono-dimensionnelles). C'est dans la forme du profil suivant les différentes directions de projection qu'est contenue cette information 2D.(Transformation de Radon)[RB1]
Malheureusement, cette modélisation mathématique a été élaborée dans un contexte continu
- q prend n'importe quelle valeur dans
- u prend n'importe quelle valeur dans

C’est à partir de cette théorie que sont effectuées les reconstructions en TEP de façon standard.
Or, en pratique, on ne dispose que d'un
nombre fini de directions et u ne prend qu'un ensemble fini de valeurs
dans ![]() .
.
Si les capteurs où sont recueillis les projections ont une certaine épaisseur, la projection suivant une direction devient :

L'intégration sur une bande passe par l'utilisation de la fonction h définie par :
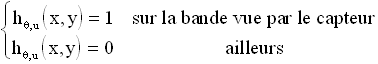
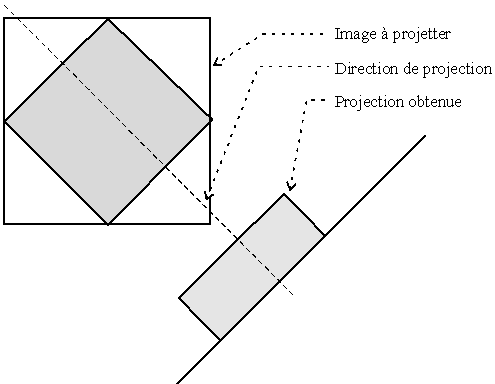
Une première géométrie valable pour modéliser la projection est donnée dans la table des illustration : figure 1.
Il est nécessaire de savoir que ce modèle n'est qu'une vision approchée de la réalité physique. Nous utiliserons dans un premier temps ce modèle de projection pour sa simplicité. Il sous-entend que les photons comptés par un capteur sont uniquement issus de la bande que "voit" celui ci. Cette hypothèse n'est pas, dans la réalité, rigoureusement exacte.
La sommation continue définie par le signe somme va être remplacée par une sommation discrète sur l'ensemble des pixels (§Visualisation de l’image 1.2.2 ). L'opération élémentaire d'une telle sommation consite à parcourir l'image, à calculer les coordonnées de chaque pixel visité et à sommer sa valeur si son centre se trouve dans la bande de projection. Du fait de la discrétisation, un certain nombre de problèmes va déjà se poser...
Considérons pour cela une image (Un carré orienté suivant une direction particulière), extrayons-en le sinogramme et regardons le profil pour une direction donnée.
Théoriquement nous aurions dû trouver une projection constante, mais, du fait des effets de crénelage au bord et des arrondis, nous obtenons un profil fortement accidenté.

Le problème se pose de manière accrue quand la bande d'intégration est relativement fine (par rapport à la résolution en pixel de l'image). En effet, normalement chaque pixel recouvert par une bande devrait contribuer à la projection en fonction de l'aire de recouvrement entre le pixel et la bande et, comme ici, non de manière binaire. Calculer la fraction de chaque pixel qui est recouvert par la bande est malheureusement fortement coûteux en temps. Ce problème est bien connu en représentation d'image (Aliasing) et des algorithmes ont été écrits pour calculer cette aire de recouvrement. [RB3]
Toutefois, ici, plutôt que d’utiliser l’un de ces algorithmes on va parcourir l'image par des incréments de taille inférieure au pixel. Si on parcourt l'image par pas de 1/n, chaque élément apporte à la projection une valeur I/n2 si I est la valeur du pixel.
Une autre méthode consiste à penser la projection de manière différente et à réaliser une interpolation. [RB17]

Dans ce contexte, la valeur du pixel cj est comptée au niveau des capteurs pi et pi+1 en fonction de la distance de ces capteurs par rapport à la ligne de coïncidence (respectivement d et 1-d ) soit :

Si cette méthode peut sembler plus séduisante, d'un point de vue informatique, il reste à s'assurer du fondement physique d'une telle interpolation.
Quoiqu’il en soit, nous avons jusqu'ici supposé que la ligne de coïncidence donnait la droite de laquelle avaient été émis les photons. Malheureusement un certain nombre de facteurs physiques rendent inexacts la localisation de cette droite. Parmis ces facteurs citons :
- Parcours du b
- Emission des photons qui ne se fait pas rigoureusement en opposition
- Effet Compton

On peut donc envisager d'utiliser un simulateur de Monte Carlo pour modéliser la projection. Celui-ci va, à partir d’un nombre fixé d’éléments radioactifs, simuler la trajectoire de ces derniers depuis le tissu cérébral jusqu’aux détecteurs. L’avantage principal est de pouvoir y intégrer les phénomènes physiques en fonction de la complexité du modèle que l’on attend. Si une telle méthode peut sembler séduisante de par sa flexibilité, elle reste lourde au niveau du temps de calcul. En effet elle utilise principalement des tirages aléatoires sur des fonctions de probabilités où la trajectoire d’une particule est suivie pas à pas de son apparition à son comptage.[RB7]
C’est pourquoi, dans un premier temps nous chercherons à utiliser des méthodes analytiques. Dans ce cas, la projection se résume à :
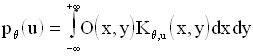
où ![]() est le noyau qui
caractérise la détection des photons du point
(x,y) pour la projection
est le noyau qui
caractérise la détection des photons du point
(x,y) pour la projection ![]() .
.
Ainsi que ce soit les effets
perturbateurs d'origine physique ou d'origine informatique
liés à la discretisation d'un problème
continu, le lien entre l'activité et la mesure, ie le
processus de projection, peut revêtir des degrés
de complexités variables suivant le modèle que
l'on s'est fixé. Il reste à définir
quel modèle est suffisant, quel noyau ![]() choisir,
lorsqu'on s'est fixé un mode de reconstruction.
choisir,
lorsqu'on s'est fixé un mode de reconstruction.
- Décomposition et Visualisation discrète d’une image
- Décomposition de l’image
- Base de Pixels
- Base de Blobs [RB9] [RB10] [RB12]
- Base transformée
- Visualisation de l’image
- Illustration d’une décomposition
- Entre Projection et Base de Reconstruction H
- Introduction
- Etablissement du Système
- Remplissage de H
- Sens de H
- Remplissage de H et information à priori
Dans la nature, les objets sont définis à l'échelle macroscopique de manière continue, et la représentation de tels objets nécessiterait une fonction O(x,y) continue, définie en chaque point (x,y) de l'espace. Les algorithmes de reconstruction, eux, ne peuvent couvrir qu'une région particulière de l'espace et même au sein de cette portion de l'espace ne produisent qu'un ensemble discret de valeurs pour représenter une image. L'image numérisée f(i,j) se résume alors à un ensemble de MxN points, considéré comme un tableau rectangulaire obtenu après échantillonage S et quantification Q de l'image originale O(x,y) à support original continu

La manière la plus fréquente de discrétiser une image consiste à moyenner l'information sur une portion de surface[RB1]. En 2D, on utilise un élément carré : le pixel. L'image se résume alors à une série de MxN pixels auxquels on affecte une valeur représentative de l'information moyenne contenue dans ce pavé. Cette série de valeurs ne donne pas une représentation exacte de O(x,y) puisque les détails de résolution inférieure à la taille du pixel sont perdus lors du moyennage.

où ![]() représente
la valeur en (i,j) de la sous image Pkl
liée au pixel indexé ij , Ckl
la valeur moyenne de cette sous image. Les sommes finies sur M et N
définissent la portion de l'espace sur laquelle on
décompose l'image originale. Ce sont les coefficients Ckl
, qui définissent l'image, qui seront stockés
dans l'ordinateur.
représente
la valeur en (i,j) de la sous image Pkl
liée au pixel indexé ij , Ckl
la valeur moyenne de cette sous image. Les sommes finies sur M et N
définissent la portion de l'espace sur laquelle on
décompose l'image originale. Ce sont les coefficients Ckl
, qui définissent l'image, qui seront stockés
dans l'ordinateur.
Nous avons décomposé l'image originale sur une base d'images élémentaires Pij pour obtenir l'image discrétisée.
Remarque :
Si de plus on considère un ordre de lecture de ce tableau bidimensionnel, ordre lexicographique par exemple, cette série de MxN valeurs peut être mise sous la forme d'un vecteur colonne.

Si cette décomposition de l'image en pixels reste la plus fréquente, elle est loin d'être la seule....
Au lieu de considérer un élément surfacique carré comme le pixel, on peut utiliser des images élémentaires basées sur une famille d’éléments à symétrie cylindrique. On définit alors une grille où chaque noeud sert de point d'ancrage à un membre de cette famille. Si la grille comporte N noeuds il y aura N images élémentaires : une par noeud. On peut montrer qu'un tel système constitue une base de décomposition.
Famille de Blobs
Les fonctions de bases, Blobs, utilisées dans cette décomposition sont une généralisation de la fenêtre de pondération de Kaiser-Bessel utilisée en traitement du signal. Une des particularités de cette famille de fonction, à la différence de celle des pixels, réside dans le fait que les images de base se recouvrent dans l’espace. Le contrôle de la continuité ainsi que celui des différentes propriétés des fonctions élémentaires de cette famille se fait par deux paramètres m (entier non négatif) et a (nombre réel). On désigne par B(m,a )(r) un membre de cette famille :

où a indique l’étendue du blob et Im la fonction de Bessel modifiée.
Il existe une littérature abondante pour l’utilisation des fonctions à symétrie de révolution dans des domaines variés (interpolation multidimensionnelle et approximation). En revanche, les fonctions décrites précédemment ont été introduites par Lewitt (1990) dans le cadre de la reconstruction d’images.
Notre image devient donc :

où Bk est un élément de la famille des Blobs centré en (ik, jk).
Nous avons jusqu’à présent décomposé l’image dans un repère " visuel "; mais nous savons qu’à cet espace de décomposition peut être associé un espace dual transformé.
Par la suite on suppose les images carrées.
Soit F(u,v) l’ensemble des N2 points du tableau bidimensionnel que forme la transformée.

La transformée directe s’obtient par :

et la transformée inverse :

où a(i,u,j,v) et b(u,i,v,j) sont les noyaux de la transformation, ou simplement des opérateurs linéaires. Ces opérateurs linéaires pourraient être quelconques, mais pour simplifier, nous les considèrerons orthogonaux et séparables. Ainsi, ils pourront s’écrire de manière équivalente :
a(i,u,j,v) = a1(i,u) . a2(j,v)
b(u,i,v,j) = b1(u,i) . b2(v,j)
Il est ainsi possible de décomposer la transformation globale bidimensionnelle en deux transformations monodimensionnelles, l’une s’appliquant sur les lignes du tableau, l’autre sur les colonnes.

De plus, pour certaines transformations, les opérateurs a et b sont égaux, ainsi que a1 et a2, ce qui permet de n’utiliser qu’un seul algorithme pour effectuer les transformations directes et inverses.
On peut ré-écrire l’image discrétisée f(i,j) par :

ou encore

L’image f(i,j) est donc vue comme la somme pondérée par F(u,v) des sous images au(i)av(j.).
En d’autre termes, les transformations induites par les noyaux au et av opèrent un changement de base de la représentation de f(i,j), où l’on passe d’un repère visuel dans lequel chaque composante représente un degré de luminance d’un point d’image donné, à un repère " transformé " de même dimension N2 mais où cette fois la base de représentation est composée de N2 sous images et où chaque composante représente le poids de cette sous-image dans l’image f(i,j).
Il existe de nombreuses transformées orthogonales. La plus connue et la plus naturelle est la transformée de Fourier, base de l’analyse spectrale. Pour la transformée de Fourier discrète, le noyau de la transformation s’exprime par
![]()
obtenu en considérant la fonction périodique formée par la répétition du vecteur à coder :
M1 M2 M3 M4 M1 M2 M3 M4 M1 ......
Lorsqu’on rend la fonction à la fois périodique et paire en fabriquant la suite
M1 M2 M3 M4 M4 M3 M2 M1 M1...
seuls les termes en cosinus sont non nuls, on obtient la transformée en cosinus dont les coefficients sont :

De même, la transformée en sinus est la transformée de Fourier obtenue en rendant la fonction impaire.
On peut s’arrêter quelques instants à l’intérêt de passer dans un tel espace transformé.....
L’image échantillonnée, nous l’avons vu, se résume dans le cas d’images carrées à un tableau bidimensionnel de dimension N2. Ces échantillons sont toutefois statistiquement dépendants et l’information se trouve répartie sur l’ensemble de l’image.
Dans le cas d’une base transformée, le changement d’espace de représentation produit une condensation de l’énergie. Si maintenant on regarde l’évolution de l’énergie des coefficients en fonction de leur rang on s’aperçoit que celle-ci décroit rapidement.

La transformation va donc concentrer l’information sur un ensemble réduit de coefficients. Autrement dit, si après transformation l’image est effectivement représentée par un tableau de N2 coefficients, on pourra en conserver un nombre M<N2 en ne détériorant que de façon raisonnable l’image.
Bien souvent après reconstruction d’une image, il est nécessaire d’afficher les résultats. La visualisation de cette image passe par l’utilisation d’un moniteur vidéo qui va afficher une série de points sur l’écran. Il est fréquent dans ce cas la de parler de pixels pour désigner la " résolution " de l’image affichée. On parlera d’image de 128*128 pixels. Même si par ce terme pixel, on désigne également une entité élémentaire, il s’agit d’une portion de l’écran et non de l’espace réel. On prendra donc bien soin de ne pas confondre les pixels écrans(Espace de Représentation) avec les pixels formant une base de décomposition de f(i,j). En effet, il sera possible de décomposer l’image sur une base de Fourier et ensuite d’en construire une image 128*128 pixels
Quelle que soit la base de décomposition de l’image, on a vu que l’image pouvait s’exprimer comme une somme pondérée de sous-images.
On trouve dans la table des illustrations, une représentation de quelques unes des images élémentaires pour les bases mentionnées au paragraphe 1.2.1. Figure 2.

Nous nous sommes attachés dans un premier temps à la modélisation de la projection, dans un deuxième temps aux différentes bases de reconstruction, nous allons maintenant lier les deux dans l’objectif de reconstruire une image à l’aide de ses projections.
Nous disposons d’un jeu fini de projections pl, nous voulons estimer les coefficients Ck caractéristiques de l’image à reconstruire pour une certaine base.
Rappelons que d’une manière générale:
![]()

où Il représente la sous image indicée l de la base de reconstruction.
On cherche à exprimer la famille des projections {p} comme une combinaison linéaire des différents éléments de la famille {c}.
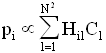
où Hil représente la contribution Cl de la sous image Il à la projection pi
Un examen, en TEP, nous fournit
pour un objet O(x,y) continu un jeu de mesures correspondant au nombre
de coups détectés par capteur. Cet objet,
après échantillonnage et quantification est
représenté par une image approchée fk.
Cette approximation de l’objet sera maintenant
considérée comme l’image originale. On
va chercher à l’estimer, et l’estimation
sera notée ![]() .
.
On souhaite que la
projection de cette estimée soit la plus proche possible des
projections obtenues par les mesures. Autrement dit, si on
réalise la projection de notre estimation ![]() on
veut que le jeu de projection obtenu soit aussi proche que possible du
jeu expérimental. Dans le cas simple de la projection
suivant une bande, le processus est modélisé par
(paragraphe 1.1) :
on
veut que le jeu de projection obtenu soit aussi proche que possible du
jeu expérimental. Dans le cas simple de la projection
suivant une bande, le processus est modélisé par
(paragraphe 1.1) :

C’est ce type de modélisation que nous allons prendre dans un premier temps pour sa simplicité. Notre approche de la projection est discrète et dans l’hypothèse où l’image est connue, une mesure de projection suivant une direction est modélisée par .:
![]()
On suppose que cette projection est en accord avec celle effectivement mesurée au niveau du capteur i.
On souhaite que la projection de
l’estimée fournisse un résultat proche
des pi. En
remplaçant dans l’expression
précédente fk
par ![]() on
obtient la projection estimée :
on
obtient la projection estimée :
![]()
En remplaçant par sa décomposition,on obtient :

En inversant l’ordre des sommations, on obtient :

Si on définit Hil par  on
aboutit au système :
on
aboutit au système :
![]()
Ce qui peut s’écrire de manière plus condensée sous forme matricielle :
![]()
Si de plus on note par B
la différence ![]() alors le système
devient :
alors le système
devient :
![]()
où B représente l’écart des projections mesurées avec les projections telles qu’elles sont modélisées. La volonté que les projections de l’estimée soient les plus proches possible des projections réelles revient à minimiser B.
C’est au sein de la matrice H qu’interviennent simulanément les mécanismes de projection et les bases de décomposition de l’image. Cette information liant les projections et l’image telle que l’on l’a définie conditionne le remplissage de la matrice H. On voit donc l’importance de cette étape avant la résolution du système, puisque H caractérise le flux de photons d’une région de l’espace jusqu’au détecteur ainsi que les caractéristiques de la détection. Cette matrice donne la contribution de la composante Cl de l’objet à la mesure pi.
Dans une base de pixel, si on regarde Hil en fonction de i, celle ci représente la " point spread " fonction du système, la lieme colonne de H donne la réponse (ensemble de réponse des détecteurs) d’une source ponctuelle située en l.
Attendu l’information contenue dans H, on va chercher à conditionner au mieux le remplissage de H. D’où l’idée d’incorporer de l’information a priori lors du calcul de H. [RB4]
Au lieu de remplir H suivant : ![]()
on va ajouter une
pondération : ![]()
Cela revient à définir une nouvelle base de décomposition contrainte par une fonction de pondération wk. L’image élémentaire n’est plus Ikl mais Ilkwk. Dans le cas d’une base de pixels, l’élément de surface ne sera pas un plan mais une nappe définie par la matrice de contrainte. (Table des illustrations Figure 3)
