




Next: 3.3 Discrétisation du Volume.
Up: 3. Géométrie du Sinogramme.
Previous: 3.1 Introduction.
Contents
Index
3.2 Le Référentiel.
La caméra est constituée d'un ensemble de couronnes formant un cylindre. Du
fait de la propagation des photons  en opposition, nous pouvons,
par symétrie diviser l'espace d'acquisition en deux sous-espaces
en opposition, nous pouvons,
par symétrie diviser l'espace d'acquisition en deux sous-espaces  et
et  (Fig.4.1).
(Fig.4.1).
Figure 4.1:
Division de l'espace d'acquisition en deux.
|
|
Le choix du plan séparant ces deux sous-espaces est arbitraire, du moment qu'il
contient l'axe du cylindre. La subdivision revient à orienter la droite 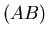 joignant deux détecteurs
joignant deux détecteurs  et
et  en ne comptant que les LOR allant
de
en ne comptant que les LOR allant
de  vers
vers  . En effet, le nombre de paires de photons
détecté suivant
. En effet, le nombre de paires de photons
détecté suivant 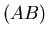 est le même que celui détecté suivant
est le même que celui détecté suivant  .
Un événement correspond à deux photons en opposition.
.
Un événement correspond à deux photons en opposition.
On associe au cylindre un repère  orthonormé
orthonormé
 d'origine
d'origine 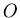 , centre géométrique
du cylindre (Fig.4.2).
, centre géométrique
du cylindre (Fig.4.2).
Figure:
Modélisation géométrique de la caméra.

|

|

|
|
[Couronne]
|
[Ligne de Coïcidence]
|
[Repère sphérique]
|
L'axe des  (axe défini par
(axe défini par  ) de ce référentiel coïncide
avec l'axe du cylindre.
) de ce référentiel coïncide
avec l'axe du cylindre.  et
et  définissent respectivement
les axes des
définissent respectivement
les axes des  et des
et des  . Ils appartiennent donc à un plan transaxial.
Nous pouvons, dans ce repère, référencer l'objet à imager. Cet objet correspond
à une distribution radioactive
. Ils appartiennent donc à un plan transaxial.
Nous pouvons, dans ce repère, référencer l'objet à imager. Cet objet correspond
à une distribution radioactive
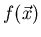 qui à chaque point
qui à chaque point
 de l'espace affecte une quantité
de l'espace affecte une quantité  représentative de la radioactivité.
Dans ce repère, la LOR
représentative de la radioactivité.
Dans ce repère, la LOR 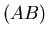 définit une droite de vecteur directeur unitaire
définit une droite de vecteur directeur unitaire
 . Deux angles
. Deux angles
 sont nécessaires pour caractériser
totalement ce vecteur
sont nécessaires pour caractériser
totalement ce vecteur  (Coordonnées sphériques).
(Coordonnées sphériques).
 définit l'angle de vue. Du fait de la subdivision de l'espace
en deux sous espaces (
définit l'angle de vue. Du fait de la subdivision de l'espace
en deux sous espaces (
 ).
).
 définit l'angle correspondant à l'inclinaison. Pour décrire totalement
l'espace il faudrait que
définit l'angle correspondant à l'inclinaison. Pour décrire totalement
l'espace il faudrait que
![$ \phi \in [-\frac{\pi }{2},\frac{\pi }{2}] $](img254.png) . Or,
du fait de la nature cylindrique du système d'acquisition, l'intervalle de valeur
décrit par cette variable est limité à
. Or,
du fait de la nature cylindrique du système d'acquisition, l'intervalle de valeur
décrit par cette variable est limité à
![$ \phi \in [-\phi _{max},\phi _{max}] $](img255.png) ,
où
,
où
 définit l'angle maximal d'inclinaison.
définit l'angle maximal d'inclinaison.
Un plan  , normal à ce vecteur
, normal à ce vecteur  peut
alors être construit. La LOR intercepte ce plan en un point
peut
alors être construit. La LOR intercepte ce plan en un point  . Il faut
deux vecteurs unitaires
. Il faut
deux vecteurs unitaires
 dans ce plan pour référencer
dans ce plan pour référencer
 . On définit donc un repère
. On définit donc un repère  du plan
du plan  par
par
 .
.  est un vecteur appartenant à un
plan transaxial (parallèle au plan définit par
est un vecteur appartenant à un
plan transaxial (parallèle au plan définit par  et
et  ).
).
 lui est orthogonal et
lui est orthogonal et  peut être choisi n'importe où
sur la droite de vecteur directeur
peut être choisi n'importe où
sur la droite de vecteur directeur  passant par l'origine
passant par l'origine  .
Toute LOR
.
Toute LOR 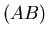 conduit dans
conduit dans
 à un point
à un point  unique
de coordonnées
unique
de coordonnées
 . Chaque LOR est donc totalement référencée
dans l'espace par le quadruplet
. Chaque LOR est donc totalement référencée
dans l'espace par le quadruplet
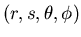 . Le sinogramme correspondant
à une acquisition en 3D à 4 dimensions ! Ce quadruplet nous permet, dans le
repère associé au cylindre, de décrire totalement la droite représentative de
la ligne de réponse
. Le sinogramme correspondant
à une acquisition en 3D à 4 dimensions ! Ce quadruplet nous permet, dans le
repère associé au cylindre, de décrire totalement la droite représentative de
la ligne de réponse  . Un point
. Un point  appartient à cette droite
s'il existe
appartient à cette droite
s'il existe
 tel que
tel que
 .
.





Next: 3.3 Discrétisation du Volume.
Up: 3. Géométrie du Sinogramme.
Previous: 3.1 Introduction.
Contents
Index
Lecomte Jean François
2002-09-07
![]() en opposition, nous pouvons,
par symétrie diviser l'espace d'acquisition en deux sous-espaces
en opposition, nous pouvons,
par symétrie diviser l'espace d'acquisition en deux sous-espaces ![]() et
et ![]() (Fig.4.1).
(Fig.4.1).
![]() orthonormé
orthonormé
![]() d'origine
d'origine ![]() , centre géométrique
du cylindre (Fig.4.2).
, centre géométrique
du cylindre (Fig.4.2).
 .
.