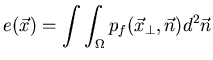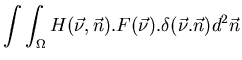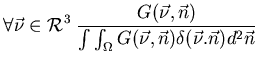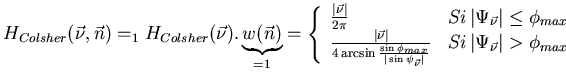Next: 6.2 Ce qu'il faut
Up: 6. Reconstruction Analytique.
Previous: 6. Reconstruction Analytique.
Contents
Index
Subsections
La solution analytique du problème d'inversion, permettant de retrouver une
image 2D  à partir de ses projections
à partir de ses projections
 , est
un problème connu et résolu depuis plus de 80 ans par un mathématicien autrichien
(Radon 1917). Si on prend le temps d'en rappeler les rudiments ici, c'est que
le cas bidimensionnel contient en lui même les fondements du problème plus complexe
que constitue la reconstruction 3D. En effet, les opérations de filtrage, de
rétroprojection, le théorème de la section centrale sont des composantes présentes
aussi bien en 2D qu'en 3D. La reconstruction 2D représentant une version allégée
du cas 3D, nous traiterons ultérieurement les problèmes inhérents au seul cas
du 3D.
, est
un problème connu et résolu depuis plus de 80 ans par un mathématicien autrichien
(Radon 1917). Si on prend le temps d'en rappeler les rudiments ici, c'est que
le cas bidimensionnel contient en lui même les fondements du problème plus complexe
que constitue la reconstruction 3D. En effet, les opérations de filtrage, de
rétroprojection, le théorème de la section centrale sont des composantes présentes
aussi bien en 2D qu'en 3D. La reconstruction 2D représentant une version allégée
du cas 3D, nous traiterons ultérieurement les problèmes inhérents au seul cas
du 3D.
6.1.1.1 La projection.
Dans la première partie de cette thèse, nous avons, de manière approfondie,
cherché à modéliser le lien qui unit l'objet radioactif à ses projections. Lorsqu'on
se place dans un contexte continu, nous avons montré que chaque élément du sinogramme
 comptabilisait les nombres de paires de photons
comptabilisait les nombres de paires de photons  émises par l'objet radioactif
émises par l'objet radioactif  suivant la ligne de coïncidence
référencée par
suivant la ligne de coïncidence
référencée par
 . Il s'agissait d'une projection.
En termes mathématiques, on considère que
. Il s'agissait d'une projection.
En termes mathématiques, on considère que
 intègre l'information
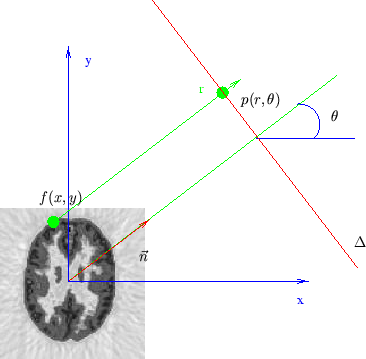
relative à cet objet sur une droite (Fig.7.1):
intègre l'information
relative à cet objet sur une droite (Fig.7.1):
où 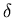 , distribution de Dirac traduit l'intégration sur la droite
de projection.
, distribution de Dirac traduit l'intégration sur la droite
de projection.
Figure:
Modélisation de la projection analytique en 2D.
|
|
Nous sommes donc capable de construire un sinogramme partant d'une distribution
de radioactivité. Comme en pratique, les imageurs TEP ne nous donnent accès
qu'au sinogramme, il faut bien, pour obtenir des images, résoudre le problème
inverse. La reconstruction consiste donc partant d'un sinogramme
 à estimer la distribution
à estimer la distribution  . Il devient donc indispensable de définir
la rétroprojection.
. Il devient donc indispensable de définir
la rétroprojection.
6.1.1.2 La rétroprojection.
L'opération de rétroprojection correspond en fait à un épandage. La rétroprojection
élémentaire permet de construire à partir
d'une projection suivant un angle  une fonction
une fonction
 .
Cette fonction est obtenue en affectant à chaque point
.
Cette fonction est obtenue en affectant à chaque point  le nombre
de paires de photons émises
le nombre
de paires de photons émises
 .
.  indique l'abscisse
où se projette ce point suivant une direction
indique l'abscisse
où se projette ce point suivant une direction  (
(
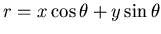 ).
La rétroprojection élémentaire conduit donc à:
).
La rétroprojection élémentaire conduit donc à:
Ce processus est illustré Fig.7.2.
Figure:
Illustration de la rétroprojection en 2D.
|
|
Cette opération élémentaire nous permet de définir la rétroprojection, opération
qui consiste à sommer l'ensemble de ces rétroprojections élémentaires pour toutes
les directions de projections possibles:
Cette sommation nous conduit à une image  , image d'épandage, qui
même si elle n'est pas loin de l'image que l'on cherche (à une convolution près)
n'est pas notre distribution finale. Il nous manque un élément: Le théorème
de section-centrale (coupe-tranche).
, image d'épandage, qui
même si elle n'est pas loin de l'image que l'on cherche (à une convolution près)
n'est pas notre distribution finale. Il nous manque un élément: Le théorème
de section-centrale (coupe-tranche).
Ce théorème, dont la preuve peut être trouver dans [66], traduit un
lien entre la transformée de Fourier 1D(
![$ P(\nu _{r},\theta )=TF_{1D}[p(r,\theta )] $](img802.png) )
des projections
)
des projections
 et la transformée de Fourier 2D (
et la transformée de Fourier 2D (
![$ F(\nu _{x},\nu _{y})=TF_{2D}[f(x,y)] $](img803.png) )
de l'objet
)
de l'objet  .
.
Figure:
Théorème de section centrale en 2D.
![\resizebox*{0,45\textwidth}{!}{\psfrag{nur}[][][1]{\textcolor{red}{\( \nu _{r} \...
...g{p(r,g)}[][][1]{\( p(r,\theta ) \)}\includegraphics{imgps/coupe_tranche2d.eps}}](img804.png)
|
![\resizebox*{0,45\textwidth}{!}{\psfrag{nur}[][][1]{\textcolor{red}{\( \nu _{r} \...
...{p(r,g)}[][][1]{\( p(r,\theta ) \)}\includegraphics{imgps/coupe_tranche2d2.eps}}](img805.png)
|
| [Espace de l'objet.] |
[Espace des fréquences.] |
Ce théorème (Fig.7.3) stipule que la transformée de Fourier 1D
des projections échantillonne suivant une direction définie par  l'espace de Fourier de l'objet. Si
l'espace de Fourier de l'objet. Si
 traduit la transformée de Fourier 2D de l'objet exprimée en coordonnées polaires,
alors le théorème de section centrale se traduit mathématiquement par:
Nous disposons maintenant de toutes les définitions nécessaires à la reconstruction
de notre image
traduit la transformée de Fourier 2D de l'objet exprimée en coordonnées polaires,
alors le théorème de section centrale se traduit mathématiquement par:
Nous disposons maintenant de toutes les définitions nécessaires à la reconstruction
de notre image  .
.
Pour reconstruire notre image partant de sa transformée de Fourier exprimée
en coordonnées polaires, nous utilisons la définition de la transformée de Fourier:
En divisant cette intégrale en deux:
Si dans le deuxième terme de cette expression, je change  par
par
 , j'obtiens pour celle-ci:
Pour des raisons de symétrie évidente (Fig.7.3), nous avons
, j'obtiens pour celle-ci:
Pour des raisons de symétrie évidente (Fig.7.3), nous avons
 ,
et comme
,
et comme
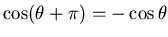 et
et
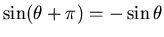 ,
nous obtenons pour ce second terme:
,
nous obtenons pour ce second terme:
En rassemblant maintenant les deux termes de 7.1, on obtient pour
l'expression de la transformée de Fourier:
 |
(6.2) |
De cette expression, par application du théorème de section centrale et en mettant
en évidence certaines portions, on arrive finalement:
L'image  s'obtient donc comme la rétroprojection, non pas des projections
simples, mais des projections filtrées
s'obtient donc comme la rétroprojection, non pas des projections
simples, mais des projections filtrées
 .(Eq.7.3).
Le filtre est simple, et nous avons directement son expression dans le domaine
fréquentiel: il s'agit du filtre monodimensionnel rampe
.(Eq.7.3).
Le filtre est simple, et nous avons directement son expression dans le domaine
fréquentiel: il s'agit du filtre monodimensionnel rampe
 .
L'algorithme de reconstruction comporte donc deux étapes:
.
L'algorithme de reconstruction comporte donc deux étapes:
- Filtrage monodimensionnel des projections dans l'espace de Fourier
 .
.
- Rétroprojection des projections filtrées
Il porte donc le nom de rétroprojection des données filtrées ou
filtered-backprojection (FBP).
D'un point de vue totalement théorique, les opérateurs utilisés étant tous linéaires,
il n'y a pas de contradiction à rétroprojeter les projections et à filtrer l'image
épandue  ensuite par un filtre rampe bidimensionnel
ensuite par un filtre rampe bidimensionnel
 ,
nous avons alors:
,
nous avons alors:
Cet algorithme porte le nom de rétroprojection filtrée ou backprojection-filtering
(BPF). En pratique, on filtre les
projections avant de les rétroprojeter car la rétroprojection est ainsi limitée
par le volume d'intérêt [84].
N'en déplaise aux puristes de la langue française, il faut noter une faiblesse
de la langue française pour traduire la différence entre ces deux algorithmes
de manière simple, c'est pourquoi les acronymes utilisés (FBP et BPF) seront
construits sur les noms des algorithmes exprimés en langue anglaise.
6.1.1.5 Filtre de reconstruction et filtre d'apodisation.
Nous venons de voir que pour reconstruire notre image, nous étions amenés à
utiliser le filtre rampe
 . L'utilisation de ce
filtre rampe pose deux problèmes majeurs:
. L'utilisation de ce
filtre rampe pose deux problèmes majeurs:
- Le support de la fonction représentant le filtre rampe n'est pas borné, ce qui
pose évidemment des problèmes dans un milieu discret.
- Cette fonction n'est pas majorée.
Afin de remédier à ces deux problèmes, l'idée consiste à conserver la forme
de la rampe fréquentielle pour les petites fréquences et de l'atténuer pour
les fréquences plus élevées. Il s'agit de choisir judicieusement la fréquence
seuil  à partir de laquelle le filtre atténuera la rampe. Il
faut garder à l'esprit qu'en pratique les calculs sont effectués sur des mesures
discrètes. Par conséquent un spectre trop étendu provoquera des phénomènes de
repliement de spectres. Pour éviter cela nousdevons tronquer les composantes
spectrales situé au dessus de la fréquence de Shannon. D'autre part, une troncature
brutale dans l'espace de Fourier conduit à des ondulations dans l'espace de
l'objet. C'est pourquoi généralement, on utilise le filtre
à partir de laquelle le filtre atténuera la rampe. Il
faut garder à l'esprit qu'en pratique les calculs sont effectués sur des mesures
discrètes. Par conséquent un spectre trop étendu provoquera des phénomènes de
repliement de spectres. Pour éviter cela nousdevons tronquer les composantes
spectrales situé au dessus de la fréquence de Shannon. D'autre part, une troncature
brutale dans l'espace de Fourier conduit à des ondulations dans l'espace de
l'objet. C'est pourquoi généralement, on utilise le filtre
 où
où  est une fonction d'apodisation.
Il existe plusieurs fonctions d'apodisation possibles. Celle utilisé en routine
sur la caméra ECAT HR+ à CYCERON est la fenêtre de Hanning:
est une fonction d'apodisation.
Il existe plusieurs fonctions d'apodisation possibles. Celle utilisé en routine
sur la caméra ECAT HR+ à CYCERON est la fenêtre de Hanning:
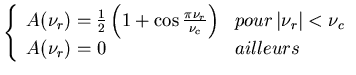
D'un point de vue physique, la fenêtre d'apodisation
 permet
de ne pas trop amplifier les hautes fréquences et donc le bruit dans les images
reconstruites.
permet
de ne pas trop amplifier les hautes fréquences et donc le bruit dans les images
reconstruites.
Dans le cas de la reconstruction d'un objet  bidimensionnel, les
projections étaient bidimensionnelles
bidimensionnel, les
projections étaient bidimensionnelles
 . Le système était
donc totalement défini analytiquement et la solution de notre système était
unique. En 3D cependant, l'intégration sur les lignes de coïncidence est spécifiée
par 4 paramètres
. Le système était
donc totalement défini analytiquement et la solution de notre système était
unique. En 3D cependant, l'intégration sur les lignes de coïncidence est spécifiée
par 4 paramètres
 . Or le volume que l'on doit reconstruire
ne comporte que trois variables
. Or le volume que l'on doit reconstruire
ne comporte que trois variables  , le problème d'inversion est
donc surdéterminé. En effet, en se limitant aux projections situées dans des
plans perpendiculaires à l'axe du cylindre (
, le problème d'inversion est
donc surdéterminé. En effet, en se limitant aux projections situées dans des
plans perpendiculaires à l'axe du cylindre ( ), nous disposons
de suffisamment d'information pour reconstruire l'objet, du moins en faisant
une reconstruction 2D tranche par tranche (i.e. en faisant varier
), nous disposons
de suffisamment d'information pour reconstruire l'objet, du moins en faisant
une reconstruction 2D tranche par tranche (i.e. en faisant varier  ).
D'un point de vue purement analytique, l'information supplémentaire apportée
par les acquisitions suivant les autres inclinaisons (
).
D'un point de vue purement analytique, l'information supplémentaire apportée
par les acquisitions suivant les autres inclinaisons (
 ) est
superflue. Enfin, cela reste vrai tant qu'on ne fait pas intervenir de considérations
statistiques ! De toute façon, cette surdétermination nous conduit à une solution
qui n'est plus unique. Idéalement, toutes les solutions conduisent à la même
estimation du volume. Malheureusement dans le monde réel, c'est-à-dire en présence
de bruit, la solution varie sensiblement. Suivant une approche proche de celle
de Defrise [30], nous allons voir les éléments qui constituent les
fondements de la reconstruction analytique 3D.
) est
superflue. Enfin, cela reste vrai tant qu'on ne fait pas intervenir de considérations
statistiques ! De toute façon, cette surdétermination nous conduit à une solution
qui n'est plus unique. Idéalement, toutes les solutions conduisent à la même
estimation du volume. Malheureusement dans le monde réel, c'est-à-dire en présence
de bruit, la solution varie sensiblement. Suivant une approche proche de celle
de Defrise [30], nous allons voir les éléments qui constituent les
fondements de la reconstruction analytique 3D.
6.1.2.1 Ensemble
 des projections.
des projections.
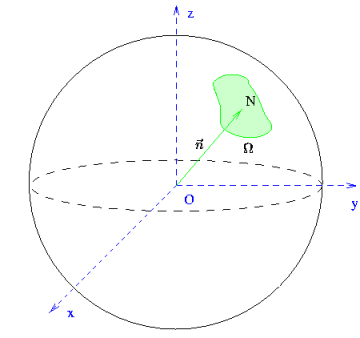
Tout plan de projection  est défini par une direction de projection
est défini par une direction de projection
 , donc par deux angles
, donc par deux angles
 . Ce vecteur
. Ce vecteur  étant un vecteur unitaire, sa norme est égale à 1. Si on prend pour représentant
de ce vecteur, le vecteur
étant un vecteur unitaire, sa norme est égale à 1. Si on prend pour représentant
de ce vecteur, le vecteur
 dont une extrémité
dont une extrémité
 est située sur l'origine du repère et si on s'intéresse au lieu géométrique
que dessine l'autre extrémité
est située sur l'origine du repère et si on s'intéresse au lieu géométrique
que dessine l'autre extrémité  lorsque
lorsque
 varient
dans
varient
dans
![$ [0,\pi ]\times [-\frac{\pi }{2},\frac{\pi }{2}] $](img836.png) , on constate que
ce point
, on constate que
ce point  décrit une sphère de rayon unité. Nous appellerons cette sphère,
la sphère des projections.
décrit une sphère de rayon unité. Nous appellerons cette sphère,
la sphère des projections.
Or l'ensemble des valeurs que peuvent prendre les deux angles  et
et  est lié à la géométrie d'acquisition. En effet, ces angles sont
fixés par les couples de détecteurs. Par conséquent, le lieu géométrique que
dessine le vecteur
est lié à la géométrie d'acquisition. En effet, ces angles sont
fixés par les couples de détecteurs. Par conséquent, le lieu géométrique que
dessine le vecteur  est fonction de la géométrie. C'est en général
un sous ensemble de la sphère des projections. C'est ce sous ensemble que nous
désignons par
est fonction de la géométrie. C'est en général
un sous ensemble de la sphère des projections. C'est ce sous ensemble que nous
désignons par  , qui constitue l'ensemble des projections. La figure
Fig.7.4
, qui constitue l'ensemble des projections. La figure
Fig.7.4
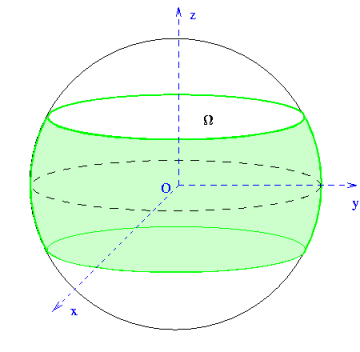
donne quelques exemples de cet ensemble  . Il faut noter que l'ensemble
des projections correspondant au cas Full 3D conduit à une géométrie
d'acquisition qui serait sphérique. Ce qui est impossible techniquement. On
note aussi que l'acquisition 2D est un cas limite, où l'ensemble
. Il faut noter que l'ensemble
des projections correspondant au cas Full 3D conduit à une géométrie
d'acquisition qui serait sphérique. Ce qui est impossible techniquement. On
note aussi que l'acquisition 2D est un cas limite, où l'ensemble  se réduit à un cercle équatorial (cercle dont le plan support passe
par le centre de la sphère de projection).
se réduit à un cercle équatorial (cercle dont le plan support passe
par le centre de la sphère de projection).
6.1.2.2 Extension du théorème de section centrale.
Comme précédemment le théorème de section centrale traduit un lien, dans l'espace
de Fourier, entre les projections et l'objet radioactif. Un plan de l'espace
de Fourier 3D de l'objet (
![$ F(\nu _{x},\nu _{y},\nu _{z})=F(\vec{\nu })=TF_{3D}[f(x,y,z)] $](img841.png) )
et perpendiculaire à la direction de projection
)
et perpendiculaire à la direction de projection  correspond à
la transformée de Fourier 2D des projections (
correspond à
la transformée de Fourier 2D des projections (
![$ P(\nu _{r},\nu _{s},\theta ,\phi )=P(\vec{\nu }_{\bot },\vec{n})=TF_{2D}[p(r,s,\theta ,\phi )] $](img842.png) )
pour cette même direction de projection (Fig.7.5).
)
pour cette même direction de projection (Fig.7.5).
Figure 7.5:
Passage des plans de projections dans l'espace de Fourier de l'objet
![\resizebox*{0,45\textwidth}{!}{\psfrag{Cercle}[][][2]{\( \Omega \)} \psfrag{x}[]...
...\)} \psfrag{PiF4}[][][2]{\( \Pi ^{F}_{4} \)}\includegraphics{imgps/rre_fig5.ps}}](img843.png)
|
![\resizebox*{0,45\textwidth}{!}{\psfrag{Cercle}[][][2]{\( \Omega \)} \psfrag{x}[]...
...\)} \psfrag{PiF4}[][][2]{\( \Pi ^{F}_{4} \)}\includegraphics{imgps/rre_fig6.ps}}](img844.png)
|
|
[Dans l'espace de l'objet.]
|
[Dans l'espace de Fourier.]
|
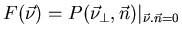 |
(6.4) |
Nous pouvons toujours décomposer le vecteur
 , comme la somme
de deux vecteurs
, comme la somme
de deux vecteurs
 et
et
 . Le premier
. Le premier
 représente un vecteur situé dans le plan perpendiculaire
au vecteur de projection
représente un vecteur situé dans le plan perpendiculaire
au vecteur de projection  (plan
(plan  de projection) . Le
deuxième
de projection) . Le
deuxième
 est colinéaire à la direction de projection
est colinéaire à la direction de projection
 . Nous avons:
. Nous avons:
Dans ce cas, il est clair que si
 , le vecteur
, le vecteur
 est un vecteur situé dans le plan perpendiculaire à la direction de projection.
De la même manière, nous pouvons définir dans l'espace de l'objet:
Partant de
est un vecteur situé dans le plan perpendiculaire à la direction de projection.
De la même manière, nous pouvons définir dans l'espace de l'objet:
Partant de  , nous avons accès aux coordonnées de la projection
dans le plan perpendiculaire à
, nous avons accès aux coordonnées de la projection
dans le plan perpendiculaire à  par
par
 .
.
Dans l'Eq. 7.4, il est nécessaire de bien comprendre l'expression:
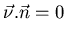 |
(6.5) |
et de voir ce qu'elle représente. Dans l'espace de Fourier de l'objet, dont
nous définissons le repère
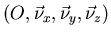 ,
si nous fixons une direction
,
si nous fixons une direction
 , le produit
scalaire précédent définit un ensemble de fréquences qui doivent être situées
dans le plan perpendiculaire à la direction
, le produit
scalaire précédent définit un ensemble de fréquences qui doivent être situées
dans le plan perpendiculaire à la direction  et passant par l'origine.
Inversement en fixant une fréquence
et passant par l'origine.
Inversement en fixant une fréquence
 , on devrait construire
un plan perpendiculaire à
, on devrait construire
un plan perpendiculaire à
 qui contient les directions de projection
qui contient les directions de projection
 vérifiant Eq.7.5. Or, d'après le paragraphe Par.7.1.2.1,
le lieu géométrique suivi par les directions de projection est également situé
sur la sphère unité. De fait, le lieu géométrique défini par les directions
vérifiant Eq.7.5 correspond à l'intersection d'un plan perpendiculaire
à
vérifiant Eq.7.5. Or, d'après le paragraphe Par.7.1.2.1,
le lieu géométrique suivi par les directions de projection est également situé
sur la sphère unité. De fait, le lieu géométrique défini par les directions
vérifiant Eq.7.5 correspond à l'intersection d'un plan perpendiculaire
à
 passant par
passant par 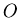 et de la sphère des projections.
et de la sphère des projections.
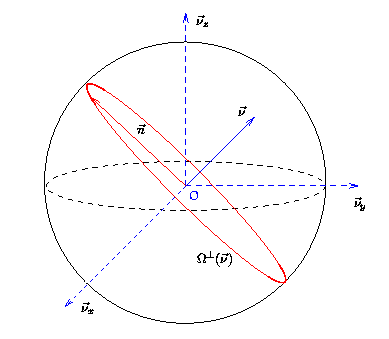
Figure:
Lieu géométrique correspondant à
 .
.
|
Ce lieu géométrique
 (Fig.7.6)
correspond à un cercle équatorial .
(Fig.7.6)
correspond à un cercle équatorial .
 correspond donc à l'ensemble des
directions de projection
correspond donc à l'ensemble des
directions de projection  pour lesquelles la fréquence
pour lesquelles la fréquence
 appartient au plan
appartient au plan  de projection construit sur
de projection construit sur  .
.
Nous avons vu également que la géométrie d'acquisition limitait les directions
de projection à  . Ainsi de manière générale, l'équation Eq.7.5
fournit un jeu de directions qui correspond à l'intersection de
. Ainsi de manière générale, l'équation Eq.7.5
fournit un jeu de directions qui correspond à l'intersection de  et
et
 . Muni de ces deux ensembles, nous pouvons
maintenant comprendre les conditions suffisantes qu'il faut imposer pour pouvoir
reconstruire.
. Muni de ces deux ensembles, nous pouvons
maintenant comprendre les conditions suffisantes qu'il faut imposer pour pouvoir
reconstruire.
6.1.2.4 Les conditions d'Orlov. [70]
Du fait du théorème de section centrale, l'objet à imager
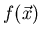 est déterminé, si dans l'espace de Fourier, nous disposons de l'information
est déterminé, si dans l'espace de Fourier, nous disposons de l'information
 pour toutes les fréquences
pour toutes les fréquences
 . De par l'équation
Eq.7.5, il faut pour chaque fréquence
. De par l'équation
Eq.7.5, il faut pour chaque fréquence
 que l'intersection
entre
que l'intersection
entre  et
et
 soit non nulle.
soit non nulle.
Il doit exister au moins une direction  qui construit
dans l'espace de Fourier un plan contenant cette fréquence !
qui construit
dans l'espace de Fourier un plan contenant cette fréquence !
Nous venons de le voir, toute direction correspond à une cercle équatorial unique,
Le théorème d'Orlov est donc le suivant:
La reconstruction de l'objet est possible si tout cercle équatorial
à au moins une intersection non vide avec l'ensemble des projections possibles
 .
.
Si on reprend les exemples d'ensembles de projections illustrés sur la Fig.7.7,
Figure 7.7:
Exemples d'ensemble de projections
 .
.
[ quelconque.] quelconque.]
|
[ relatif à une acquisition 2D.] relatif à une acquisition 2D.]
|
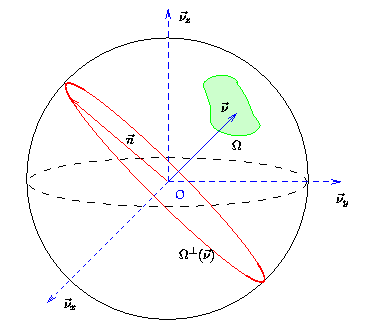
|

|
[ relatif à une acquisition sphérique (Full 3D).] relatif à une acquisition sphérique (Full 3D).]
|
[ relatif à une acquisition cylindrique.] relatif à une acquisition cylindrique.]
|

|
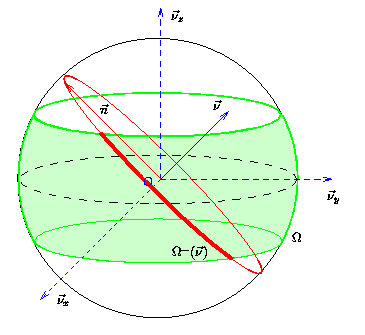
|
on constate que le premier exemple Fig.7.7.a ne permet pas de
reconstruction car on peut construire des cercles équatoriaux qui n'intersectent
pas le domaine  . En revanche, les autres cas autorisent tous la
reconstruction de l'objet.
. En revanche, les autres cas autorisent tous la
reconstruction de l'objet.
Arrêtons nous quelques instants sur le cas limite de l'acquisition 2D. Pour
toute fréquence
 (
(
 ), le
cercle équatorial
), le
cercle équatorial
 intercepte l'ensemble des projections
intercepte l'ensemble des projections
 (qui correspond lui aussi à un cercle équatorial) en 2 points.
Cela revient à dire qu'il existe 2 directions de projection pour lesquelles
le plan
(qui correspond lui aussi à un cercle équatorial) en 2 points.
Cela revient à dire qu'il existe 2 directions de projection pour lesquelles
le plan  contient la fréquence considérée. Ces deux directions sont
en opposition (180
contient la fréquence considérée. Ces deux directions sont
en opposition (180 l'une de l'autre) et sont donc équivalentes.
Elles correspondent à un même couple de détecteurs. Cela veut dire que nous
avons, pour chaque fréquence, une seule direction de projection qui contribue
à cette fréquence. Nous avons donc un rapport d'une direction pour une fréquence.
l'une de l'autre) et sont donc équivalentes.
Elles correspondent à un même couple de détecteurs. Cela veut dire que nous
avons, pour chaque fréquence, une seule direction de projection qui contribue
à cette fréquence. Nous avons donc un rapport d'une direction pour une fréquence.
Dans le cas Full 3D, l'intersection de
 et
et  conduit toujours à
conduit toujours à
 . Nous avons donc un rapport de
. Nous avons donc un rapport de 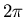 directions pour une fréquence. Ceci illustre bien la redondance des données
lorsqu'on réalise une acquisition 3D.
directions pour une fréquence. Ceci illustre bien la redondance des données
lorsqu'on réalise une acquisition 3D.
Dans ces 2 cas (acquisition 2D ou Full 3D), le rapport du nombre de projection(s)
par direction est constant quelle que soit la fréquence considérée. En revanche,
pour une acquisition cylindrique, ce ratio n'est plus constant et dépend de
la fréquence considérée. En effet, l'intersection de
 et
et  conduit à un arc de cercle, dont la longueur dépend de la
fréquence. Or le ratio fréquence/coupure est justement lié à cette longueur.
Ainsi, dans ce cas pratique fréquent, il est nécessaire de prendre en compte
la variabilité de la redondance au moment de la reconstruction, i.e. l'intégrer
à notre filtre de reconstruction.
conduit à un arc de cercle, dont la longueur dépend de la
fréquence. Or le ratio fréquence/coupure est justement lié à cette longueur.
Ainsi, dans ce cas pratique fréquent, il est nécessaire de prendre en compte
la variabilité de la redondance au moment de la reconstruction, i.e. l'intégrer
à notre filtre de reconstruction.
Nous considérons le cas de la reconstruction par FBP. Evidemment et comme son
nom l'indique, nous avons d'abord une étape de filtrage suivie d'une rétroprojection.
Le filtrage des données ne consiste plus uniquement en un simple filtre rampe
car il doit intégrer la variabilité des redondances.
Chaque projection est filtrée.
 représente
le noyau de filtrage, que nous spécifierons par la suite, exprimé dans l'espace
de Fourier. Le filtrage se traduit juste par une multiplication:
représente
le noyau de filtrage, que nous spécifierons par la suite, exprimé dans l'espace
de Fourier. Le filtrage se traduit juste par une multiplication:
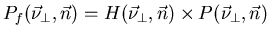 |
(6.6) |
Où la transformée de Fourier s'obtient par l'application de :
Comme précédemment, la rétroprojection consiste à affecter à la position  la valeur du sinogramme en
la valeur du sinogramme en
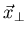 (endroit où se projette ce
point) pour l'ensemble
(endroit où se projette ce
point) pour l'ensemble  des directions.
des directions.
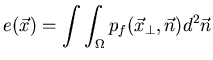 |
(6.7) |
où
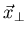 représente la projection de
représente la projection de  sur un
plan de projection perpendiculaire à
sur un
plan de projection perpendiculaire à  .
.
Le noyau de filtrage n'est pas unique. Pour le trouver, écrivons la fonction
de transfert de l'ensemble du processus que représente la mesure des projections,
leur filtrage et leur rétroprojection. Pour cela, réécrivons la rétroprojection
Eq.7.7 dans l'espace de Fourier:
où la fonction de Dirac 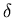 nous permet de ne sélectionner dans l'espace
de Fourier, uniquement les fréquences
nous permet de ne sélectionner dans l'espace
de Fourier, uniquement les fréquences
 perpendiculaire à la
direction de projection
perpendiculaire à la
direction de projection  . Pour une fréquence
. Pour une fréquence
 ,
cela nous conduit à une intégration curviligne sur
,
cela nous conduit à une intégration curviligne sur
 .
En utilisant l'expression du filtrage des projections Eq.7.6
et le théorème de section centrale, nous obtenons:
.
En utilisant l'expression du filtrage des projections Eq.7.6
et le théorème de section centrale, nous obtenons:
Dans l'espace de Fourier, pour que la rétroprojection des données filtrées nous
permette de remonter à l'objet, il suffit de poser
 pour
toutes les fréquences
pour
toutes les fréquences
 . Le filtre de projection prend donc
en compte le fait que les arcs
. Le filtre de projection prend donc
en compte le fait que les arcs
 ne sont pas
égaux pour toutes les fréquences. Ainsi, la solution générale conduit à toute
fonction
ne sont pas
égaux pour toutes les fréquences. Ainsi, la solution générale conduit à toute
fonction
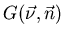 normalisée par l'intégration de ces valeurs
sur l'arc
normalisée par l'intégration de ces valeurs
sur l'arc
 [30]:
[30]:
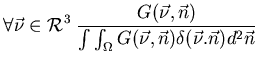 |
(6.8) |
Choisir un filtre correspond donc à choisir une fonction  qui vérifie
la propriété Eq.7.8. Parmis ces filtres, on distingue les
filtres
qui vérifie
la propriété Eq.7.8. Parmis ces filtres, on distingue les
filtres
 qui sont à
variables séparables. Pour ces filtres factorisables,
les opérations de filtrage et rétroprojection peuvent être permutées et le choix
de la fonction
qui sont à
variables séparables. Pour ces filtres factorisables,
les opérations de filtrage et rétroprojection peuvent être permutées et le choix
de la fonction
 , fonction positive est indifférent. Tous les
filtres conduisent à la même reconstruction en l'absence de données bruitées.
En présence de bruit, les filtres se comportent de manières différentes. Nous
allons maintenant décrire le filtre que nous utiliserons par la suite dans nos
reconstructions analytiques par rétroprojection des données filtrées.
, fonction positive est indifférent. Tous les
filtres conduisent à la même reconstruction en l'absence de données bruitées.
En présence de bruit, les filtres se comportent de manières différentes. Nous
allons maintenant décrire le filtre que nous utiliserons par la suite dans nos
reconstructions analytiques par rétroprojection des données filtrées.
Le filtre que nous utiliserons fut développé au départ par Colsher [21].
Ce filtre nécessite au départ un angle d'acceptance suivant la direction  qui soit constant et limité. Nous avons vu Ch.4 ce que représentait
l'angle d'acceptance axial. Cet angle n'est pas réellement constant dans notre
cas, puisque suivant le segment envisagé, les plans pairs et les plans impairs
n'intègrent pas l'information sur le même nombre de plans de détecteurs. D'autre
part, du fait de la géométrie d'acquisition cylindrique, certaines projections
sont incomplètes. Supposons néanmoins que l'angle d'acceptance est borné par
qui soit constant et limité. Nous avons vu Ch.4 ce que représentait
l'angle d'acceptance axial. Cet angle n'est pas réellement constant dans notre
cas, puisque suivant le segment envisagé, les plans pairs et les plans impairs
n'intègrent pas l'information sur le même nombre de plans de détecteurs. D'autre
part, du fait de la géométrie d'acquisition cylindrique, certaines projections
sont incomplètes. Supposons néanmoins que l'angle d'acceptance est borné par
 de la sorte que toutes les directions de projections soient
telles que l'angle
de la sorte que toutes les directions de projections soient
telles que l'angle  associé à la direction de projection vérifie
associé à la direction de projection vérifie
 . Dans ce cas, le filtre se met sous la forme:
. Dans ce cas, le filtre se met sous la forme:
Dans cette expression
 désigne l'angle que fait le
vecteur
désigne l'angle que fait le
vecteur
 avec l'axe porté par
avec l'axe porté par
 dans l'espace des fréquences (Fig.7.6). On trouvera de plus amples
renseignements sur la façon dont est obtenue ce filtre dans [21]
et sur l'implémentation dans [20].
dans l'espace des fréquences (Fig.7.6). On trouvera de plus amples
renseignements sur la façon dont est obtenue ce filtre dans [21]
et sur l'implémentation dans [20].
Jusqu'à présent, nous avons supposé que les projections suivant une direction
 sont totalement mesurée. Or, du fait de la géométrie cylindrique
d'acquisition, certaines vues sont manquantes. Pour détourner ce problème, Kinahan
et Rogers ont proposé un algorithme basé sur une reprojection d'une estimée
initiale [51]. On la calcule en utilisant uniquement les projections
du sinogramme correspondant à des directions transaxiales (
sont totalement mesurée. Or, du fait de la géométrie cylindrique
d'acquisition, certaines vues sont manquantes. Pour détourner ce problème, Kinahan
et Rogers ont proposé un algorithme basé sur une reprojection d'une estimée
initiale [51]. On la calcule en utilisant uniquement les projections
du sinogramme correspondant à des directions transaxiales ( ).
L'ensemble de ces projections répond aux conditions d'Orlov. Partant de ces
projections et par l'utilisation d'un algorithme de reconstruction par rétroprojection
2D des données filtrées, on reconstruit un premier volume (=estimée initiale).
Ce volume est ensuite projeté afin de compléter les vues manquantes du sinogramme.
Le sinogramme alors complet sert ensuite à la reconstruction 3D. Cette procédure
est illustrée Fig.7.8.
).
L'ensemble de ces projections répond aux conditions d'Orlov. Partant de ces
projections et par l'utilisation d'un algorithme de reconstruction par rétroprojection
2D des données filtrées, on reconstruit un premier volume (=estimée initiale).
Ce volume est ensuite projeté afin de compléter les vues manquantes du sinogramme.
Le sinogramme alors complet sert ensuite à la reconstruction 3D. Cette procédure
est illustrée Fig.7.8.
Figure 7.8:
Principe de la reconstruction 3D avec prise en compte des vues manquantes[4].
|
|
Par la suite, lorsque nous parlerons de reconstruction analytique standard,
nous entendrons la rétroprojection filtrée utilisant le filtre de Colsher. Nous
nous placerons toujours juste après les différentes corrections, et l'algorithme
utilisé pour obtenir une image partant de ce sinogramme corrigé est illustré
Alg.1.






Next: 6.2 Ce qu'il faut
Up: 6. Reconstruction Analytique.
Previous: 6. Reconstruction Analytique.
Contents
Index
Lecomte Jean François
2002-09-07
 des projections.
des projections.
 .
.


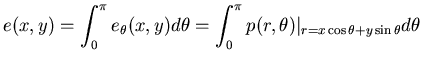
![\resizebox*{0,45\textwidth}{!}{\psfrag{nur}[][][1]{\textcolor{red}{\( \nu _{r} \...
...g{p(r,g)}[][][1]{\( p(r,\theta ) \)}\includegraphics{imgps/coupe_tranche2d.eps}}](img804.png)
![\resizebox*{0,45\textwidth}{!}{\psfrag{nur}[][][1]{\textcolor{red}{\( \nu _{r} \...
...{p(r,g)}[][][1]{\( p(r,\theta ) \)}\includegraphics{imgps/coupe_tranche2d2.eps}}](img805.png)
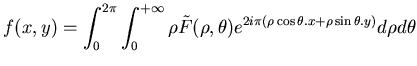


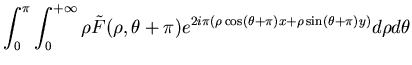

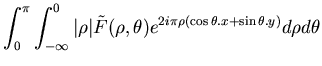

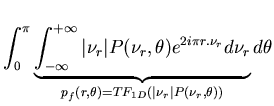
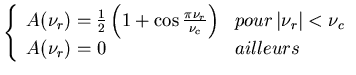


![\resizebox*{0,45\textwidth}{!}{\psfrag{Cercle}[][][2]{\( \Omega \)} \psfrag{x}[]...
...\)} \psfrag{PiF4}[][][2]{\( \Pi ^{F}_{4} \)}\includegraphics{imgps/rre_fig5.ps}}](img843.png)
![\resizebox*{0,45\textwidth}{!}{\psfrag{Cercle}[][][2]{\( \Omega \)} \psfrag{x}[]...
...\)} \psfrag{PiF4}[][][2]{\( \Pi ^{F}_{4} \)}\includegraphics{imgps/rre_fig6.ps}}](img844.png)