A.1 Un peu de Physique.

Lorsqu'on s'intéresse aux interactions existant entre les électrons et les photons, on distingue 3 grands types possibles en fonction de l'énergie mise en jeu par les photons (Fig.A.1).Classés par ordre d'énergie croissante, on observe :

• Effet Photoélectrique.
• Diffusion Compton.
• Création de Paire.

  Figure: Interaction et énergie.

  

A.1.1 Création de Paire.

C'est le type d'interaction qui prédomine quand l'énergie du photon est supérieure à $2m_{0}c^{2}=1.02MeV$.

$$\gamma \longrightarrow {e^{+}}+{e^{-}}$$

En présence d'un noyau permettant la conservation de la quantité de mouvement, un photon $\gamma$ peut spontanément donner naissance à une paire positon-électron. Le noyau va prendre la quantité de mouvement du photon, tandis que l'énergie sera acquise par la paire positon-électron.

A.1.2 L'effet photoélectrique.

En 1886, Heinrich Hertz a remarqué que la lumière ultraviolette était susceptible d'arracher des électrons d'un métal. Un minimum d'énergie $E_{i}$ est requis pour pouvoir extraire un électron d'un atome (ionisation). Cette énergie correspond à l'énergie de liaison des électrons périphériques dans l'atome. L'énergie en excès par rapport à $E_{i}$ va se retrouver sous forme d'énergie cinétique. Si un photon d'énergie $E$ suffisante vient frapper la surface d'un solide et que $E$ est absorbée par un électron, ce dernier va perdre cette énergie cinétique acquise sous la forme de collisions en se frayant un chemin vers l'extérieur. Plus l'électron est proche de la surface moins il perdra d'énergie pour sortir du solide. Les électrons qui s'échappent du solide ont donc des énergies allant de $0$ à $(E-E_{i})$. L'énergie maximale $E_{m}$ acquise par l'électron est indépendante de l'intensité des photons incidents et dépend de la fréquence de ces derniers. L'intensité jouant uniquement sur le nombre d'électrons qui vont être emis et non sur leur énergie cintique.

$$E_{m}=E-E_{i}=h\nu -E_{i}$$

où $h$ est la constante de Planck. Merci á Einstein pour l'interprétation de ce phénomène (1905).

A.1.3 La diffusion Compton.

A.1.3.1 De quoi s'agit-il?

Pour mettre en évidence ce processus physique, on peut réaliser la même expérience que celle que réalisa Compton en l'an de grâce 1923 (Fig.A.2).

Figure A.2: Effet Compton

Dans cette expérience, un photon incident d'énergie $E_{0}$ (de longueur d'onde $\lambda _{0}$) va diffuser suivant un angle $\theta$ après interaction, collision avec un électron. Du fait de cette collision, l'énergie du photon passe de $E_{0}$ à $E_{1}$. Par application de la:

A.1.3.1.1 Conservation de l'énergie

$$E_{0}+m_{0}c^{2}=E_{1}+E_{e}$$ (A.1)

où $m_{0}c^{2}$ représente l'énergie au repos de l'électron, et $E_{e}$ l'énergie cinétique de recul de ce même électron du fait de l'interaction.

A.1.3.1.2 Conservation de la quantité de mouvement

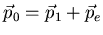$$\vec{p}_{0}=\vec{p}_{1}+\vec{p}_{e}$$ (A.2)

où $p_{i}$ représente la quantité de mouvement associée à chacune des particules en mouvement. Comme l'énergie du photon est liée à la quantité de mouvement par $E=pc$ où $c$ est la vitesse de la lumière et en utilisant (A.2), on tire :

$$p_{e}^{2}=p_{1}^{2}+p_{0}^{2}-2p_{0}p_{1}\cos {\theta }$$

et donc

$$c^{2}p_{e}^{2}=E_{0}^{2}+E_{1}^{2}-2E_{0}E_{1}\cos {\theta }$$

En remplaçant dans (A.1), on obtient après manipulation :

$$E_{1}=\frac{E_{0}}{1+\frac{E_{0}}{m_{0}c^{2}}(1-\cos {\theta })}$$ (A.3)

A l'aide de (A.3) on voit que l'énergie du photon incident est modifiée par l'interaction qu'il a subi. La perte d'énergie est fonction de l'angle de diffusion compton. Mais cette équation ne nous permet pas de définir quel sera l'énergie à la sortie. A priori, rien ne nous dit, en effet, avec quelle angle la diffusion a eu lieu. Il faudrait, a minima, connaître la probabilité qu'a chaque photon incident de diffuser avec l'angle $\theta$. Une manière de quantifier cela passe par l'utilisation de la section efficace de diffusion.

A.1.3.2 Section efficace de diffusion

A.1.3.2.1 Notions préliminaires

Angle Solide

La donnée d'un cône de sommet O équivaut à la donnée de sa section par la sphère de centre O et de rayon 1. Par définition, la surface de la calotte sphérique $S_{1}$ est appelé angle solide . Il est exprimé en stéradian(Fig A.3).

Figure A.3: Angle Solide

Soit le cône porté par une section cylindrique dont les génératrices font un angle $\alpha$ avec $OC$. Lorsque on parcours $\theta =[0,\alpha ]$, on intercepte la calotte sphérique suivant plusieurs cercle dont le rayon va de $CB=CA=R\sin {\theta }$à $0$ en $H$. En intégrant pour chaque $\theta$ les différents périmètres, on trouve la valeur de l'angle solide pour un angle quelconque du cône.

$$\Omega (\alpha ) =\int _{0}^{\alpha }{2\pi R\sin {\theta }d\theta }$$

$$=2\pi R(1-\cos {\alpha })$$

1. L'angle $\alpha =\pi$ correspond à tout l'espace et comme l'angle solide est ramenéà la sphère unité $R=1$, sa valeur est alors de $4\pi$ stéradians.
2. L'angle solide sert à caractériser une portion d'espace qui est vue suivant une certaine ouverture angulaire à partir d'un point. C'est l'équivalent 3D de l'angle en 2D.

Section efficace

La section efficace est une notion qui permet de quantifier l'effet d'un obstacle sur le chemin d'un faisceau. Lorsqu'un obstacle (une personne par exemple) intercepte un faisceau (par exemple la lumière du soleil), il interagit avec une partie de ce faisceau et seulement une partie de ce dernier va se projeter sur une surface (l'ombre de la personne sur le sol). Cette surface représente la section efficace. C'est donc une mesure du taux d'interaction d'un objet avec un faisceau.

A.1.3.2.2 Section efficace de diffusion

Afin de comprendre ce que recouvre ce terme et de voir la signification de cette grandeur, on va faire des hypothèses simplificatrices, qui évitent d'introduire des notions de mécaniques quantiques nécessaires pour le calcul la section efficace de diffusion. Considérons la Fig.A.4 où $\phi _{0}$, exprimé en $cm^{2}/s$ est le flux incident de photons ayant la même énergie. $\phi _{1}$ représente la fraction de $\phi _{0}$ qui traverse l'écran sans avoir interagi.

Figure A.4: Section efficace de diffusion

On cherche à calculer le nombre d'interaction dans un petit volume de l'écran (Volume $V$) dans un intervalle de temps $T$. Le nombre d'interactions $n_{i}$ est proportionnel :

1. au flux $\phi _{0}$ incident de photons. Plus le nombre de photons qui arrivent est grand, plus le nombre d'interactions est grand.
2. à l'intervalle de temps considéré$T$.
3. au nombre de cibles dans le volume considéré : $V\times N$ où$N$ est la densité de cibles par unité de volume.

De fait :

$$n_{i}=\phi _{0}TVN\sigma (E_{0})$$ (A.4)

où la constante de proportionnalité $\sigma (E_{0})$ qui représente le taux d'interaction de la cible avec le flux de photons est appelée section efficace exprimée en $cm^{-2}$. En effet, d'après (A.4) la constante de proportionnalité est homogène à une surface. On fait ici l'hypothèse que le nombre de cibles est petit, constant, de sorte que le flux reste constant sur l'intervalle de temps considéré. Le flux considéré est un flux scalaire qui dépend de l'énergie des photons.

Le rapport $P=\frac{n_{i}}{VN}$ représente la probabilité pour une cible de l'écran d'interagir avec un photon. Dans ce cas :

$$\sigma (E_{0})=\frac{P}{T\phi _{0}(E_{0})}$$

Suivant le type d'interaction que l'on cherche à caractériser, on va décomposer la section efficace en sous section

$$\sigma (E_{0})=\sum _{i}\sigma _{i}(E_{0})$$

où la section efficace $\sigma _{i}$ qui caractérise le taux de photons qui diffusent par effect Compton est appelée section efficace de diffusion. Il est évident que le flux de photon ne correspond pas forcément à un flux de photons parallèles, on introduit donc une notion de section efficace différentielle $\frac{d\sigma }{d\Omega }$ où $d\Omega$ représente une portion élémentaire d'angle solide. Par intégration, on trouve la section efficace de diffusion dans une portion de l'espace.

A.1.4 Probabilité de diffusion

Klein et Nishina ont donné en 1929 l'expression de la section efficace différentielle de diffusion compton :

$$\frac{d\sigma }{d\Omega }(\theta ) = \frac{r_{0}^{2}}{2}\frac{1+\cos ^{2}\theta }{(1+\frac{E_{0}}{m_{0}c^{2}}(1-\cos \theta ))^{2}}\times$$

$$\left( 1+\frac{\left( \frac{E_{0}}{m_{0}c^{2}}\right) ^{2}(1-\cos... ...)^{2}}{(1+\cos ^{2}\theta )(1+\frac{E_{0}}{m_{0}c^{2}}(1-\cos \theta ))}\right)$$ (A.5)

Dans notre cas, les photons incidents ont une énergie de $E_{0}=511keV$, ce qui correspond à l'énergie au repos de l'électron et donc (A.3) devient :

$$E_{1}=\frac{E_{0}}{2-\cos \theta }$$

et (A.5) devient:

$$\frac{d\sigma }{d\Omega }(\theta )=\frac{r_{0}^{2}}{2}\frac{1+\co... ...eft( 1+\frac{(1-\cos \theta )^{2}}{(1+\cos ^{2}\theta )(2-\cos \theta )}\right)$$ (A.6)

Si maintenant, on s'intéresse aux photons diffusés en 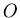$O$ suivant l'angle $[\theta ,\theta +d\theta ]$ par rapport à un axe, on cherche à exprimer la section efficace pour cet angle de diffusion. Elle s'obtient en intégrant sur l'angle solide que sous-tend cet angle dans l'espace. Or nous avons vu préalablement, qu'une façon naturelle de paramètrer l'angle solide revient à considérer un angle (Ici $\theta$) par rapport au centre d'un cône (Fig.A.3). La portion d'angle solide $d\Omega$ que sous tend la portion d'angle de diffusion $d\theta$ est donc tout simplement:

$$d\Omega =2\pi \sin \theta d\theta$$

Ainsi, pour connaître la section efficace de diffusion pour un angle solide défini par des génératrices faisant un angle $\alpha$ avec un axe, on intégre (A.5) pour $\theta$ appartenant à $[0,\alpha ]$.

$$\sigma (\alpha )=\int _{S_{1}}\frac{d\sigma }{d\Omega }(\theta )\... ... _{0}^{\alpha }\frac{d\sigma }{d\Omega }(\theta )\, 2\pi \sin {\theta }d\theta$$

Soit :

$$\sigma (\alpha ) = \pi r_{0}^{2}\left( \frac{9}{2}-{1\over {{2{\left( -2+\cos (\alpha )\right) }^{2}}}}\right.$$

$$\left. +{3\over {-2+\cos (\alpha )}}-\cos (\alpha )-3\, \log (2-\cos (\alpha ))\right)$$ (A.7)

La section efficace relative à l'espace tout entier s'obtient en fixant $\alpha =\pi$, on trouve alors :

$$\sigma (\pi )=\pi r_{0}^{2}\left( \frac{40}{9}-3\log (3)\right)$$

Cette constante permet une normalisation. On peut donc à partir du taux d'interaction (A.5) définir une densité de probabilité d'interaction:

$$f(\theta )=\frac{1}{\sigma (\pi )}\frac{d\sigma (\theta )}{d\Omega }$$

Celle ci représente pour un photon, la probabilité dans une direction particulière de l'espace, de diffuser suivant un angle compris entre $\theta$ et $\theta +d\theta$. L'intégration de cette dernière (A.7) nous donne la fonction de répartition correspondante $F(\alpha )$. Ces deux grandeurs sont représentées sur la figure (A.5).

Figure: Probabilité de diffusion