A.2 Le cas de la TEP

Les interactions photon-matière que nous avons définies précédemment interviennent en TEP à deux niveaux différents :

• Dans la matière présente dans le champ de vue. Les interactions dans l'air peuvent être considérées comme négligeables.
• Au niveau des détecteurs.

Du fait de la nature différente de ces deux types de milieu, l'intéraction prépondérante dans chacun de ces 2 cas sera elle aussi différente (A.6). Compte tenu des énergies de photons mises en jeu, la création de paire sera constamment négligée.

Figure: Coefficient d'atténuation linéique en $cm^{-1}$ du diffusé Compton (+) et de l'effet photoélectrique (x).

[Détecteur BGO]

[Cerveau]

A.2.1 Au niveau des détecteurs

A.2.1.0.1 Efficacité des détecteurs

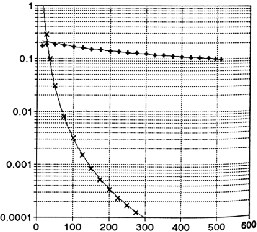
A $511keV$, effet photoélectrique et Compton sont tous deux importants (Fig. A.6.a). Tout photon qui entre dans les détecteurs est analysé individuellement. C'est la quantité d'énergie que le photon va délivrer au sein du détecteur qui est importante. Il peut soit libérer toute son énergie par effet photoélectrique, soit seulement une partie dans le cas de la diffusion Compton. C'est cette énergie déposée qui permet la scintillation, c'est la scintillation qui, après photomultiplication et traitements, permet de créer une impulsion électrique proportionnelle à lénergie déposée. On comprend donc que l'effet photoélectrique est fortement souhaité parceque l'énergie des photons issue de l'annihilation est totalement communiquée au détecteur en une fois. En revanche, du fait des intéractions Compton, un photon $E_{0}$ peut être détecté avec une énergie plus faible. Il peut également libérer son énergie en plusieurs fois et dans des détecteurs différents. L'efficience du détecteur, i.e. son aptitude à détecter les photons incidents, est principalement fonction du cristal scintillateur, de la géométrie du détecteur et de l'énergie du photon incident.

A.2.1.0.2 Résolution en énergie

Le détecteur doit être en mesure de discriminer l'énergie déposée par chaque photon. La résolution en énergie correspond à la réponse du système de détection à une source monoénergétique. Elle est bien modélisée de façon simple, par une fonction Gaussienne $f_{E_{1}}(E)$ dont la moyenne est l'énergie du photon incident $E_{1}$ et dont la variance est calculée en utilisant celle des détecteurs à $511keV$, définie de manière empirique.

$$\sigma _{E_{1}}^{2}=\sigma _{511}^{2}\sqrt{\frac{E_{1}}{511}}$$

$f_{E_{1}}(E)dE$ nous donne la probabilité pour un photon incident d'énergie $E_{1}$ d'être détecté dans $[E,E+dE]$. La probabilité de détecter un photon d'énergie $E_{1}$ dans une fenêtre d'énergie définie par deux bornes $E_{l}<E_{u}$ est donnée par l'intégration de cette probabilité. ^A.1

$$P_{E_{1}} = \int _{E_{1}}^{E_{u}}f(E)dE$$

$$= \frac{1}{\sigma _{E_{1}}\sqrt{2\pi }}\int _{E_{l}}^{E_{u}}exp\left( -\frac{(t-E_{1})^{2}}{2\sigma _{E_{1}}^{2}}\right) dt$$

$$= \frac{1}{2}erfc\left[ \frac{E_{l}-E_{1}}{\sqrt{2}\sigma _{E_{1}}}\right] -\frac{1}{2}erfc\left[ \frac{E_{u}-E_{1}}{\sqrt{2}\sigma _{E_{1}}}\right]$$ (A.8)

Le modèle gaussien, sur lequel s'appuie le calcul de cette probabilité (A.8), est simple mais suffisant pour prendre en compte l'angle d'incidence, la pénétration dans le cristal, et le pouvoir de discrimination des détecteurs.

A.2.2 Dans la matière du champ de vue

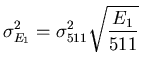
A ce niveau, c'est l'effet compton qui est prédominant (Fig A.6.b). Il faut également noter que dans l'effet photoélectrique le photon disparait purement et simplement, tandis que dans le cas de la diffusion Compton il est simplement dévié et perd une partie de son énergie. De manière assez générale, lors de la reconstruction d'image TEP, chaque évènement du sinogramme correspond à la détection quasi-simultanée de 2 photons. C'est sur la droite (LOR) joignant ces deux détecteurs qu'est supposée avoir eu lieu l'annihilation. On comprend donc bien que toute déviation dans le trajet de l'un des deux photons du lieu d'emission jusqu'au capteur va venir altérer la localisation de cette droite. Par ailleurs, d'une manière globale sur une grand nombre de désintégrations et suivant une direction particulière, l'effet photoélectrique, la création de paires et l'effet Compton se manifestent par un nombre de photons détectés qui va être inférieur au nombre de photons effectivement émis. Pour caractériser cette perte, on passe par l'utilisation d'un coefficient d'atténuation.

Figure A.7: Absorption suivant une direction dans une tranche $dx$

Suivant une direction de propagation du photon, dans une tranche $dx$ du milieu, le nombre de photons qui disparaissent est directement lié au nombre de cibles $n(x)$ dans le milieu.(Fig.A.7). On trouve donc :

$$dn(x)=-\mu (x)n(x)dx \Leftrightarrow \frac{dn(x)}{n(x)}=-\mu (x)dx$$

$$\Rightarrow n(x)=\exp \left( -\int \mu (x)dx\right)$$

où $\mu (x)$, le coefficient d'atténuation linéique, caractérise dans une direction, le taux de photons qui disparaissent par tranche $dx$ et dépend du matériau traversé. A une constante de normalisation près cette expression permet de définir la probabilité pour un photon de traverser un matériau sans disparaître. Lors de son trajet, le photon peut interagir de 3 sortes et disparaître de cette direction de propagation, on décompose ainsi le coefficient d'atténuation en trois contributions :

$$\mu =\tau (Photo\acute{e}lectrique)+\sigma (Compton)+\kappa (Paires)$$