




Next: B. L'algorithme OSEM-OSL et
Up: A. Diffusion.
Previous: A.2 Le cas de
Contents
Index
Nous venons de voir, une à une, les principales briques qui constituent
la physique des processus de diffusion que subissent les photons, ainsi que
les spécificités de la TEP, nous pouvons maitenant essayer de construire
un simulateur analytique de ce processus dans un examen TEP.
Figure A.8:
Notations pour la simulation
|
|
On considère une ligne de coincidence, i.e. on donne deux capteurs situés
en  et
et  . On se fixe un volume émetteur (Fig.A.8).
Chaque point
. On se fixe un volume émetteur (Fig.A.8).
Chaque point 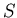 de ce volume est susceptible de correspondre à un
site où une diffusion a eu lieu. La ligne de coincidence originale
de ce volume est susceptible de correspondre à un
site où une diffusion a eu lieu. La ligne de coincidence originale ![$ [BC] $](img1595.png) est donc altérée. On ne considère que la diffusion simple ( i.e.
lorsque un seul des deux photons emis en coincidence est diffuse et ne subit
qu'une interaction). Une fois
est donc altérée. On ne considère que la diffusion simple ( i.e.
lorsque un seul des deux photons emis en coincidence est diffuse et ne subit
qu'une interaction). Une fois  et
et  donnés, le point
donnés, le point 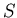 correspond à une diffusion suivant un angle
correspond à une diffusion suivant un angle
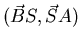 bien précis pour qu' après avoir été deviés par diffusion,
les photons soient détectés par les 2 capteurs
bien précis pour qu' après avoir été deviés par diffusion,
les photons soient détectés par les 2 capteurs  et
et  .
Si l'angle est fixé, l'énergie du photon délivrée sur les
détecteurs est, elle aussi, bien déterminée. En chaque point
S, on va donc chercher le nombre moyen
.
Si l'angle est fixé, l'énergie du photon délivrée sur les
détecteurs est, elle aussi, bien déterminée. En chaque point
S, on va donc chercher le nombre moyen  de paires de photons émis
dans le volume qui vont diffuser en S et observé au niveau de la ligne
de coincidence
de paires de photons émis
dans le volume qui vont diffuser en S et observé au niveau de la ligne
de coincidence  . Il y a deux possibilités suivant que le point
d'émission des 2 photons avant diffusion en
. Il y a deux possibilités suivant que le point
d'émission des 2 photons avant diffusion en 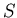 est situé sur
le trajet
est situé sur
le trajet ![$ [AS] $](img1597.png) où
où ![$ [BS] $](img1598.png) . On suppose pour expliquer le calcul
que l'émission a lieu sur le trajet
. On suppose pour expliquer le calcul
que l'émission a lieu sur le trajet ![$ [BS] $](img1598.png) .
.
Pour estimer  , il faut connaître :
, il faut connaître :
- Le nombre d'éléments radioactifs susceptibles de donner une émission
dans la direction considérée
![$ [BS] $](img1598.png) . Il est donné par l'intégration
sur le long du chemin
. Il est donné par l'intégration
sur le long du chemin
![$ S_{B}=[SI_{B}] $](img1599.png) de la densité
de la densité de
traceur radioactif.
de
traceur radioactif.
- La probabilité pour ces éléments radioactifs d'émettre dans
l'angle solide que représente la surface
 du détecteur vue
du point de diffusion
du détecteur vue
du point de diffusion 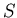 . L'émission est isotrope donc a lieu dans
. L'émission est isotrope donc a lieu dans
 stéradians. La portion dans l'angle solide du détecteur
s'obtient par règle de trois
où
stéradians. La portion dans l'angle solide du détecteur
s'obtient par règle de trois
où
 est la surface du détecteur
est la surface du détecteur  et
et  la distance qui sépare le point de diffusion
la distance qui sépare le point de diffusion 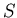 du détecteur.
du détecteur.
- La probabilité pour ces photons de parcourir le parcours
 .
Elle s'obtient facilement en considérant le facteur d'atténuation
linéique
.
Elle s'obtient facilement en considérant le facteur d'atténuation
linéique  .
.
- La probabilité de diffusé suivant l'angle
 dans l'angle solide que représente la surface du détecteur
dans l'angle solide que représente la surface du détecteur  vues du point de diffusion
vues du point de diffusion 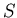 . Elle s'obtient grâce au calcul de
Klein et Nishina
où
. Elle s'obtient grâce au calcul de
Klein et Nishina
où
 est la surface du détecteur
est la surface du détecteur  et
et  la distance qui sépare le point de diffusion
la distance qui sépare le point de diffusion 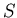 du détecteur.
La probabilité est considérée constante sur l'angle solide lié
au détecteur.
du détecteur.
La probabilité est considérée constante sur l'angle solide lié
au détecteur.
- La probabilité pour le photon diffusé de parcourir le trajet
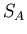 .
Elle s'obtient facilement en considérant le facteur d'atténuation
linéique
.
Elle s'obtient facilement en considérant le facteur d'atténuation
linéique  .
.
- La probabilité pour les 2 photons d'être détectés par les
capteurs
 et
et  . On la calcule en faisant l'hypothèse simple
d'une résolution en énergie qui est gaussienne. On trouve d'après
(A.8) :
. On la calcule en faisant l'hypothèse simple
d'une résolution en énergie qui est gaussienne. On trouve d'après
(A.8) :





Next: B. L'algorithme OSEM-OSL et
Up: A. Diffusion.
Previous: A.2 Le cas de
Contents
Index
Lecomte Jean François
2002-09-07

![]() et
et ![]() . On se fixe un volume émetteur (Fig.A.8).
Chaque point
. On se fixe un volume émetteur (Fig.A.8).
Chaque point ![]() de ce volume est susceptible de correspondre à un
site où une diffusion a eu lieu. La ligne de coincidence originale
de ce volume est susceptible de correspondre à un
site où une diffusion a eu lieu. La ligne de coincidence originale ![]() est donc altérée. On ne considère que la diffusion simple ( i.e.
lorsque un seul des deux photons emis en coincidence est diffuse et ne subit
qu'une interaction). Une fois
est donc altérée. On ne considère que la diffusion simple ( i.e.
lorsque un seul des deux photons emis en coincidence est diffuse et ne subit
qu'une interaction). Une fois ![]() et
et ![]() donnés, le point
donnés, le point ![]() correspond à une diffusion suivant un angle
correspond à une diffusion suivant un angle
![]() bien précis pour qu' après avoir été deviés par diffusion,
les photons soient détectés par les 2 capteurs
bien précis pour qu' après avoir été deviés par diffusion,
les photons soient détectés par les 2 capteurs ![]() et
et ![]() .
Si l'angle est fixé, l'énergie du photon délivrée sur les
détecteurs est, elle aussi, bien déterminée. En chaque point
S, on va donc chercher le nombre moyen
.
Si l'angle est fixé, l'énergie du photon délivrée sur les
détecteurs est, elle aussi, bien déterminée. En chaque point
S, on va donc chercher le nombre moyen ![]() de paires de photons émis
dans le volume qui vont diffuser en S et observé au niveau de la ligne
de coincidence
de paires de photons émis
dans le volume qui vont diffuser en S et observé au niveau de la ligne
de coincidence ![]() . Il y a deux possibilités suivant que le point
d'émission des 2 photons avant diffusion en
. Il y a deux possibilités suivant que le point
d'émission des 2 photons avant diffusion en ![]() est situé sur
le trajet
est situé sur
le trajet ![]() où
où ![]() . On suppose pour expliquer le calcul
que l'émission a lieu sur le trajet
. On suppose pour expliquer le calcul
que l'émission a lieu sur le trajet ![]() .
.
![]() , il faut connaître :
, il faut connaître :


 dans l'angle solide que représente la surface du détecteur
dans l'angle solide que représente la surface du détecteur 
![$\displaystyle \epsilon _{A}(E_{1})=\epsilon _{B}(E_{1})=\frac{1}{2}erfc\left[ \...
...ght] -\frac{1}{2}erfc\left[ \frac{E_{u}-E_{1}}{\sqrt{2}\sigma _{E_{1}}}\right] $](img1612.png)