2.2 Paramètres d'une caméra TEP.

2.2.1 Résolution spatiale.

Soit $d$ la distance entre 2 sources ponctuelles. Il existe une valeur minimale de $d$ en dessous de laquelle les sources ponctuelles ne sont plus discernables après reconstruction. Cette distance définit la résolution spatiale. On la définit comme la largeur totale à mi hauteur de la réponse impulsionnelle de la caméra. Cette résolution spatiale globale est influencée par :

• Le parcours du positon avant annihilation variable suivant l'isotope.
• La faible dispersion angulaire des photons émis autour de 180$^{\circ }$.
• La taille des détecteurs ainsi que le couplage entre les cristaux et les PM. (résolution intrinsèque)
• La pénétration oblique des photons $\gamma$ qui peuvent alors traverser plusieurs cristaux avant d'interagir.
• Les procédures d'échantillonnage et de filtrage appliquées lors de la reconstruction.

Pour évaluer la résolution, on utilise des sources émettrices linéaires. Ces sources sont disposées à différents endroits du champ de vue. La résolution correspond aux LTMH des différents profils obtenus (fréquemment approximés par des gaussiennes) dans les trois dimensions [86].^2.1

2.2.2 Taux de comptage.

Par sensibilité, on entend le rapport entre le nombre d'événements vrais enregistrés par unité de temps et la concentration radioactive effectivement présente dans le champ de vue. C'est donc la quantité d'informations acquises à partir de laquelle l'image doit être reconstruite. On l'exprime usuellement en fréquence d'événements (évnt/s) par concentration d'activité (Bq/ml). Il faut noter que l'optimisation de la sensibilité se fait en général au détriment de la résolution spatiale. En effet la sensibilité dépend également de la taille et de la disposition des détecteurs [74].

A faible activité, le taux de comptage de coïncidences vraies varie linéairement avec l'activité alors que le taux de comptage des coïncidences fortuites varie selon le carré de l'activité [32,45]. Cependant, la montée du signal lumineux et sa décroissance, la formation du signal électronique par le PM, puis le traitement subi entraîne un temps mort pendant lequel le système ne peut pas compter de nouveaux événements. Si l'intervalle de temps moyen séparant l'arrivée de deux événements est grand devant ce temps mort, la variation du taux de comptage en coïncidence vraies en fonction de l'activité reste effectivement linéaire. En revanche, lorsque l'activité est telle que l'intervalle de temps moyen séparant l'arrivée de deux événements est du même ordre de grandeur que la durée du temps mort, il apparaît une non-linéarité qui traduit une perte de comptage.

Pour décrire les performances d'un imageur TEP, il est bon de mentionner :

• la sensibilité intrinsèque représentant les capacités de comptage à faible activité.
• la valeur maximale de comptage effectivement atteinte et l'activité à laquelle elle survient (capacité de comptage à haute activité).

2.2.3 Bruit dans les images reconstruites.

Lors d'une acquisition, on cherche à compter le nombre de photons $\gamma$ détectés simultanément suivant des lignes de coïncidence. L'ensemble de ces mesures constitue le sinogramme. Or, nous avons vu Par.3.1.3.1 que:

• des coïncidences fortuites et diffusées venaient s'ajouter aux coïncidences vraies.
• des photons disparaissaient purement et simplement (atténuation).

2.2.3.1 Coïncidences supplémentaires.

Les coïncidences supplémentaires ne font qu'introduire un bruit lors de la reconstruction. Il est donc indispensable de les estimer au mieux pour pouvoir en corriger les effets. On définit la fraction de diffusés Compton $\alpha _{D}$ et la fraction de fortuites $\alpha _{F}$ avec

$$\alpha _{D} = \frac{N_{D}}{N_{V}+N_{D}+N_{F}}$$

$$\alpha _{F} = \frac{N_{F}}{N_{V}+N_{D}+N_{F}}$$

où $N_{V}$, $N_{F}$, $N_{D}$ représentent respectivement le nombre de coïncidences vraies, fortuites et diffusées.

2.2.3.1.1 Les coïncidences fortuites.

Elles affectent principalement les basses fréquences de l'image. Les méthodes de corrections reposent sur la soustraction d'une valeur constante. Cette dernière représente la contribution estimée des fortuits au nombre total d'événements enregistrés sur chaque ligne de coïncidence. Elle peut être évaluée à partir du taux de comptage de photons isolés reçus par chaque détecteur. Le taux de fortuits $T_{F}$ (nombre de coïncidences fortuites par unité de temps) est donc tel que :

$$T_{F}\approx T_{1}\times T_{2}\times \tau$$

où $\tau$ représente la durée de la fenêtre de coïncidence, et $T_{1}$et $T_{2}$ sont les taux de comptage (par unité de temps) de photons isolés des deux détecteurs en coïncidences considérés. L'avantage de cette méthode est la faible erreur introduite, car le taux de comptage élevé pour les photons isolés assure une bonne robustesse statistique.

2.2.3.2 Les coïncidences diffusées.

Par diffusion Compton dans le milieu imagé, certaines lignes de coïncidences sont faussées. La fraction de ces photons surtout pour une acquisition 3D sans septa est importante. En effet la probabilité pour des photons $\gamma$ d'énergie 511 keV d'interagir dans des tissus humains est élevée. Elle entraîne une dégradation du contraste et de la résolution des images, qu'il est difficile de minimiser et de corriger. En effet, la diffusion dépend à la fois de l'objet imagé et de la géométrie d'acquisition. il suffit de voir le nombre de méthodes proposées et envisagées pour se rendre compte que la correction du diffusé est complexe. On peut distinguer les méthodes de corrections suivant qu'elles interviennent avant, pendant où après la reconstruction. Nous n'évoquerons ici que la première catégorie. Pour cette seule catégorie, il est encore nécessaire de distinguer :

• Les méthodes qui s'appuient sur des seuils d'énergie [48,17]. L'idée est de mesurer de façon parallèle les détections dans différentes fenêtres d'énergie et ainsi de pouvoir discriminer et classer les photons. En effet, chaque fois qu'un photon interagit par diffusion, il cède une partie de son énergie. Ces algorithmes s'appuient sur la différence de forme du spectre d'énergie des photons suivant qu'ils ont diffusés où non. Ce filtrage sur l'énergie est parfois difficilement réalisable pour les détecteurs, étant donné leur résolution énergétique grossière.
• Les méthodes de type ``déconvolution-soustraction'' [11,83,65,59]. La contribution des diffusés est modélisée par la convolution des projections mesurées $p_{mes}$ par un noyau $N_{Dif}$:
  $$p_{dif}=p_{mes}*N_{Dif}$$
  où $*$ représente une convolution. On retrouve la contribution des événements vrais en soustrayant $p_{dif}$ à $p_{mes}$. Le noyau $N_{Dif}$ qui peut varier localement est déterminé à l'aide de sources simples connues, ou par simulations. Il est extrêmement difficile par l'utilisation de cette méthode de prendre en compte la nature géométrique de l'objet diffusant.
• Les méthodes de type Monte-Carlo qui vont simuler le transport des photons pour chaque objet émettant [7,68,67,69]. Elles peuvent intégrer le degré de réalisme souhaité (notamment géométrique), mais en contrepartie nécessitent une puissance ou un temps de calcul prohibitif.
• Les méthodes qui sont à mi-chemin entre les méthodes de type Monte-Carlo et les méthodes analytiques. Citons la méthode développée par Watson [98], qui permet de corriger les fausses détections dues au fait qu'un seul photon sur la paire a diffusé. Ce photon a de plus diffusé qu'une seule fois (Single Scatter). C'est cette méthode qui est implémentée sur l'imageur que nous utilisons. Elle part d'une reconstruction 2D à faible résolution et sans correction d'un volume émetteur et d'un volume d'atténuation (Voir Par.3.2.3.3). Le volume d'atténuation est utilisé pour définir les bords de l'objet à imager. On tire au hasard quelques centaines de points à l'intérieur de ce volume. Ces points seront des sites de diffusion. On ne considère ensuite qu'un sous ensemble des lignes de coïncidences. Pour chaque LOR prise dans ce sous ensemble, on va estimer la contribution de chaque site de diffusion en termes de nombre de photons qui ont diffusé. La fraction de diffusé s'exprime comme la somme des contributions sur tout le volume de tous les sites de diffusions. Le principe du calcul de la contribution d'un site de diffusion à une LOR est donné en Annexe.

2.2.3.3 Atténuation.

Dans le champ de vue, les photons peuvent disparaître par effet photoélectrique, ils sont absorbés et cèdent toute leur énergie à un électron du milieu. Si on se réduit à ce seul effet, et si on se fixe une ligne de coïncidence $M_{1}M_{2}$, une émission en un point $M$ sur cette ligne produit 2 photons $\gamma _{1}$ et $\gamma _{2}$ qui se déplacent en opposition sur cette droite. Chaque photon peut interagir par effet photoélectrique avec le milieu du champ de vue sur son parcours jusqu'aux détecteurs $M_{1}$ et $M_{2}$. Chaque photon $\gamma _{i}$ à donc une certaine probabilité $I\! \! P_{i}$ d'être détecté qui dépend du facteur d'atténuation linéique du milieu traversé (On suppose pour simplifier que le coefficient du milieu peut être considéré comme constant). Comme les parcours des photons une fois émis sont indépendants, la probabilité pour que les deux photons soient détectés simultanément par $M_{1}$et $M_{2}$ est :

$$\begin{array}{cl} I\! \! P_{1,2} & =I\! \! P_{1}\times I\! \... ...u .M_{1}M_{2}\right] \; si\: \mu \: est\: constant. \end{array}$$

On constate alors que la probabilité pour les photons d'être détectés simultanément par les détecteurs ne dépend pas de l'endroit où a eu lieu l'émission, mais plutôt de la distance parcourue dans l'objet atténuant suivant cette ligne de coïncidence. Cette propriété permet de comparer une mesure a vide avec une mesure de transmission réalisé à partir d'une source externe . On peut calculer ainsi des coefficients correcteurs $a_{M_{1}M_{2}}$ pour chaque ligne de coïncidence tel que $a_{M_{1}M_{2}}=N_{Vide}/N_{Trans}$où $N_{Vide}$, et $N_{Trans}$représentent respectivement les nombres de coups recueillis à vide où lors de la mesure de transmission [95,49,71,46]. Par simple multiplication par ce coefficients des nombres de coups recueillis pendant un examen d'émission, on peut effectuer une correction d'atténuation. En dépit de sa simplicité, cette méthode présente certains inconvénients, il faut éviter tant que possible les mouvements de l'objet imagé (Il s'agit en général d'un sujet !). De plus, l'examen en transmission n'est pas exempt de bruit, qui va évidemment se propager sur l'image reconstruite.

2.2.3.4 Comptage à bruit équivalent (NEC).

Nous venons de voir que dans notre façon de compter les photons $\gamma$ en coïncidence, il existait de nombreuses sources d'erreur, mais ce serait oublier que durant la durée de l'examen, ces photons proviennent d'une désintégration, et qu'une telle désintégration est un processus dont la nature est intrinsèquement aléatoire. Autrement dit, pendant un intervalle de temps, le nombre de désintégrations et par conséquent le nombre de paires de photons émises est soumis à des fluctuations. Le processus d'émission des positons obéit à une statistique de Poisson. Il est clair que le nombre de positons émis est fonction de l'activité radioactive de l'objet imagé. En TEP, la nature radioactive du patient provient d'un traceur injecté ou inhalé. Il est donc nécessaire de limiter au maximum l'exposition à la radioactivité, ceci réduit évidemment le nombre de coups qui seront émis durant la durée de l'examen. Ces fluctuations statistiques sont évidemment présentes tout au long du processus d'acquisition et de reconstruction. Ce bruit présent à la source, va se propager durant toute la chaîne et va altérer le signal. Il semble donc alors essentiel de caractériser en fin de chaîne, i.e. après reconstruction, le signal restant par rapport au bruit présent dans l'image.

Une mesure globale du rapport signal/bruit a été introduite par Strother et collaborateurs [93]: il s'agit du Noise Equivalent Contraste. Ce $NEC$ représente le nombre de coïncidences vraies devant être accumulées par un tomographe parfait (sans diffusé ni fortuits) pour avoir le même rapport signal sur bruit que le tomographe réel considéré. 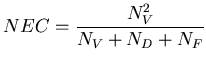Strother et collaborateurs montre que le rapport signal sur bruit au centre d'un fantôme homogène est proportionnel à la quantité

$$NEC=\frac{N^{2}_{V}}{N_{V}+N_{D}+N_{F}}$$

où $N_{V}$, $N_{F}$, $N_{D}$ représentent respectivement le nombre d'événements vrais, fortuits et diffusés collectés durant l'acquisition. L'expression précédente est modifiée et affinée en considérant la variance introduite par les corrections de la diffusion Compton et des coïncidences fortuites. On obtient:

$$NEC=\frac{N^{2}_{V}}{(1+\left[ \frac{N_{D}}{N_{D}+N_{V}}\right] ^{2}).[N_{V}+N_{D}+(1+k).N_{F}]}$$

où $k$ est une constante qui dépend de la méthode utilisée pour évaluer le nombre de fortuits. Elle vaut 0 lorsque la correction utilise le taux de comptage des photons isolés (Par.3.2.3.1). Stearns et Wack [91] ont considéré une variance supplémentaire, due à la correction de l'atténuation.

Le $NEC$ ne donne pas d'information sur le bruit en un point quelconque de l'image mais peut être utilisé pour comparer les performances de deux caméras, ou d'une même caméra pour des modes d'acquisition différents.