




Next: 7.4 Ce qu'il faut
Up: 7. Reconstruction et Rebinning.
Previous: 7.2 Dans l'espace de
Contents
Index
Subsections
7.3.1 FOurier REbinning (FORE).
Le rebinning par l'algorithme FORE proposé dès 1995 par Defrise et collaborateurs
[28] est une approche attrayante, déjà intellectuellement par la
théorie sur laquelle il s'appuie, mais aussi parcequ'il permet de s'affranchir
des problèmes de précisions (SSRB) ou de mauvais comportement en présence de
bruit (MSRB). En revanche, l'algorithme FORE ne repose pas sur des concepts
aussi simples que les autres méthodes de rebinning. Nous l'envisageons
seulement dans une approche géométrique, mais une expression exacte du rebinning
développée par Defrise [29] permet d'établir le coeur de l'algorithme
et ses limitations. L'approche théorique s'offre même le luxe d'englober le
SSRB.
Nous avons montré que dans le cas idéal, le sinogramme revenait à intégrer les
photons  sur la LOR
sur la LOR
 . Nous avons montré que le
plan de projection
. Nous avons montré que le
plan de projection  est invariant par translation suivant le vecteur
est invariant par translation suivant le vecteur
 . Le point
. Le point  de projection peut donc être choisi n'importe
où sur la LOR. Par la suite ce point est choisi à mi-chemin entre les deux détecteurs
de projection peut donc être choisi n'importe
où sur la LOR. Par la suite ce point est choisi à mi-chemin entre les deux détecteurs
 et
et  . Ceci conduit à des coordonnées faciles à calculer.
. Ceci conduit à des coordonnées faciles à calculer.
Lorsque, partant de la géométrie illustrée Fig.8.2,
Figure:
Géométrie pour la description de l'algorithme FORE.
[Une LOR  .]

[Notation dans le plan transaxial passant par  .] .]
![\resizebox*{0,45\textwidth}{!}{\psfrag{theta}[][][2]{\textcolor{blue}{\( \theta ...
...ag{n}[][][2]{\textcolor{red}{\( \vec{n} \)}}\includegraphics{imgps/rre_fig3.ps}}](img894.png) [Notation dans le plan contenant axe [Notation dans le plan contenant axe  et le point et le point  .] .]
![\resizebox*{0,45\textwidth}{!}{\psfrag{theta}[][][2]{\textcolor{blue}{\( \theta ...
...ag{n}[][][2]{\textcolor{red}{\( \vec{n} \)}}\includegraphics{imgps/rre_fig4.ps}}](img895.png)
|
nous cherchons à lier les coordonnées du point  avec les données auxquelles
nous avons accès dans un sinogramme (le quadruplet
avec les données auxquelles
nous avons accès dans un sinogramme (le quadruplet
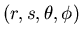 ),
nous trouvons :
),
nous trouvons :
Exprimons maintenant le vecteur directeur de la LOR:
Comme  est constant et différent de
est constant et différent de
 , nous
réécrivons ces coordonnées différemment:
Si on traduit l'intégration sur la LOR, nous obtenons:
, nous
réécrivons ces coordonnées différemment:
Si on traduit l'intégration sur la LOR, nous obtenons:
D'un autre coté, exprimons la transformée de Fourier 2D de
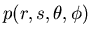 suivant les variables
suivant les variables  et
et  .
.
 |
(7.2) |
En remplaçant dans Eq.8.2,
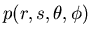 par sa
valeur dans Eq.8.1, nous obtenons:
par sa
valeur dans Eq.8.1, nous obtenons:
 |
(7.3) |
On réécrit tout cela en considérant les variables  et
et  et on
choisit
et on
choisit
 et
et
 de telle sorte que:
Comme nous reconnaissons le changement de variable associé à une rotation,
nous en déduisons que le déterminant de la matrice Jacobienne
de telle sorte que:
Comme nous reconnaissons le changement de variable associé à une rotation,
nous en déduisons que le déterminant de la matrice Jacobienne
 de ce changement de variable vaut 1 (
de ce changement de variable vaut 1 (
 ). Sachant que:
Nous en déduisons pour Eq.8.3 en permutant l'ordre des intégrations,
). Sachant que:
Nous en déduisons pour Eq.8.3 en permutant l'ordre des intégrations,
![$\displaystyle P(\nu _{r},s,\nu _{\theta },\phi )=\cos \phi .\int \int _{x,y}\un...
... -y\cos \theta ).\nu _{r}+\theta .\nu _{\theta })}d\theta \right] }_{I_{1}}dxdy$](img910.png) |
(7.4) |
Regardons de plus près ce que représente l'intégration sur les  .
.
Nous pouvons considérer l'intégrale  (Eq.8.4) comme une
somme vectorielle de complexes
(Eq.8.4) comme une
somme vectorielle de complexes
![$ \bar{z}(\theta )=A(\theta )e^{-iB(\theta )}=A(\theta )[cos(B(\theta ))+i.sin(B(\theta ))] $](img911.png) (Fig.8.3.a). Notons que le changement de signe de
(Fig.8.3.a). Notons que le changement de signe de
 fait basculer la phase. Considérons alors les cas suivants:
fait basculer la phase. Considérons alors les cas suivants:
Figure 8.3:
Principe de phase stationnaire.
[représentation du complexe
 .] .]
|
[Cas où  et et 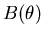 varient rapidement.] varient rapidement.]
|
[Cas où seul 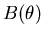 varie.] varie.]
|
[Cas où  et et 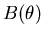 varient lentement.] varient lentement.] |
![\resizebox*{0,2\textwidth}{!}{\psfrag{A(theta)}[br][][2]{\( A(\theta ) \)} \psfrag{B(theta)}[][][2]{\( B(\theta ) \)}\includegraphics{imgps/rre_fig8.ps}}](img913.png)
|
![\resizebox*{0,2\textwidth}{!}{\psfrag{A(theta)}[br][][2]{\( A(\theta ) \)} \psfrag{B(theta)}[][][2]{\( B(\theta ) \)}\includegraphics{imgps/rre_fig9.ps}}](img914.png)
|
![\resizebox*{0,2\textwidth}{!}{\psfrag{A(theta)}[br][][2]{\( A(\theta ) \)} \psfrag{B(theta)}[][][2]{\( B(\theta ) \)}\includegraphics{imgps/rre_fig10.ps}}](img915.png)
|
![\resizebox*{0,2\textwidth}{!}{\psfrag{A(theta)}[br][][2]{\( A(\theta ) \)} \psfrag{B(theta)}[][][2]{\( B(\theta ) \)}\includegraphics{imgps/rre_fig11.ps}}](img916.png)
|
-
 et
et
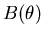 varient rapidement.(Fig.8.3.b)
Dans ce cas, on ne peut pas dire grand chose et l'intégrale
varient rapidement.(Fig.8.3.b)
Dans ce cas, on ne peut pas dire grand chose et l'intégrale  doit
être calculée explicitement.
doit
être calculée explicitement.
- Seul
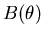 varie et
varie et
 reste relativement constant
(Fig.8.3.c). Dans ce cas, comme l'argument change vite, le
vecteur représentatif de
reste relativement constant
(Fig.8.3.c). Dans ce cas, comme l'argument change vite, le
vecteur représentatif de
 tourne rapidement. La somme
vectorielle (c'est-à-dire
tourne rapidement. La somme
vectorielle (c'est-à-dire  ) de tous ces
) de tous ces  est globalement
proche de zéro. Les vecteurs sont orientés de tous les sens mais ont la même
norme. La contribution finale est minime et
est globalement
proche de zéro. Les vecteurs sont orientés de tous les sens mais ont la même
norme. La contribution finale est minime et  est proche de 0.
est proche de 0.
- Si
 et
et
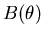 varient lentement et même à la limite
sont constants (Fig.8.3.d), alors tous les vecteurs se retrouvent
confinés dans une petite région (la phase tourne peu) et pointent dans la même
direction (il n'y a pas de changement de signe donc pas de changement de phase).
Alors, l'ensemble des éléments
varient lentement et même à la limite
sont constants (Fig.8.3.d), alors tous les vecteurs se retrouvent
confinés dans une petite région (la phase tourne peu) et pointent dans la même
direction (il n'y a pas de changement de signe donc pas de changement de phase).
Alors, l'ensemble des éléments
 agissent dans le même
sens et contribuent fortement à la somme.
agissent dans le même
sens et contribuent fortement à la somme.
Ainsi, en faisant l'hypothèse que la fonction  est relativement lisse,
donc qu'elle varie peu, du moins par rapport à la variation de la phase, nous
pouvons dire que les contributions à l'intégrale
est relativement lisse,
donc qu'elle varie peu, du moins par rapport à la variation de la phase, nous
pouvons dire que les contributions à l'intégrale  proviennent principalement
des endroits où la phase est stationnaire. Cette propriété correspond justement
au théorème de phase stationnaire [26].
Il s'agit donc de trouver les
proviennent principalement
des endroits où la phase est stationnaire. Cette propriété correspond justement
au théorème de phase stationnaire [26].
Il s'agit donc de trouver les  qui rendent cette phase stationnaire.
Pour cela, on cherche angles de vues pour lesquels
qui rendent cette phase stationnaire.
Pour cela, on cherche angles de vues pour lesquels
 .
Notons que lorsque
.
Notons que lorsque
 ,
il y a deux solutions dans l'intervalle
,
il y a deux solutions dans l'intervalle ![$ [0,2\pi ] $](img921.png) . Nous avons alors:
Cette propriété, constatée par Edholm, est remarquable. Sur la figure Fig.8.4.a,
nous avons représenté la variation de la phase
. Nous avons alors:
Cette propriété, constatée par Edholm, est remarquable. Sur la figure Fig.8.4.a,
nous avons représenté la variation de la phase
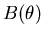 et de sa dérivée
et de sa dérivée
 . Nous allons regarder la contribution à
l'intégrale
. Nous allons regarder la contribution à
l'intégrale  des
des  appartenant soit à
appartenant soit à ![$ [3.6,3.8] $](img924.png) ,
soit à
,
soit à
![$ [2.1,2.3]. $](img925.png) Le premier intervalle correspond à des valeurs de
Le premier intervalle correspond à des valeurs de  qui rendent la dérivée de la phase maximale. Le deuxième, à des
qui rendent la dérivée de la phase maximale. Le deuxième, à des  qui donnent une variation de phase proche de
qui donnent une variation de phase proche de  . On constate dans le premier
cas illustré Fig.8.4.b. que les vecteurs
. On constate dans le premier
cas illustré Fig.8.4.b. que les vecteurs
 échantillonnent régulièrement le cercle unité. On retrouve le cas décrit Fig.8.3.c.
La contribution de cet intervalle est donc négligeable. En revanche, sur le
deuxième intervalle (phase stationnaire), les vecteurs
échantillonnent régulièrement le cercle unité. On retrouve le cas décrit Fig.8.3.c.
La contribution de cet intervalle est donc négligeable. En revanche, sur le
deuxième intervalle (phase stationnaire), les vecteurs
 sont confinés sur une petite portion du cercle unité (Fig.8.4.c),
on retrouve donc le cas décrit Fig.8.3.d. La contribution
de cet intervalle va donc être prépondérante.
sont confinés sur une petite portion du cercle unité (Fig.8.4.c),
on retrouve donc le cas décrit Fig.8.3.d. La contribution
de cet intervalle va donc être prépondérante.
Figure 8.4:
Phase stationnaire pour l'algorithme Fore.

|

|

|
[Expression de
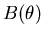 (vert) et de sa dérivée (bleu) quand (vert) et de sa dérivée (bleu) quand
 ] ]
|
[Vecteur
 lorsque lorsque
![$ \theta \in {[} 3.6,3.8 {]} $](img57.png) ] ]
|
[Vecteur
 lorsque lorsque
![$ \theta \in {[} 2.1,2.3 {]} $](img58.png) ] ]
|
Ainsi, les 2 points qui contribuent dans l'espace de Fourier au sinogramme
sont situés sur la LOR à la distance
 .
En pratique, le sinogramme intègre l'information sur de multiples LOR.
.
En pratique, le sinogramme intègre l'information sur de multiples LOR.
Cette relation de distance fréquentielle établit que toute valeur de
 de fréquence
de fréquence
 reçoit principalement
des contributions de points situés à une distance
reçoit principalement
des contributions de points situés à une distance
 sur les LOR.
sur les LOR.
Cette approximation peut en quelque sorte être vue comme un temps de
vol virtuel [29].
En appliquant ce théorème de phase stationnaire à notre équation (Eq.8.4),
i.e. en remplaçant le troisième argument de  et en sortant ce terme
de l'intégrale nous obtenons:
et en sortant ce terme
de l'intégrale nous obtenons:
![$\displaystyle P(\nu _{r},s,\nu _{\theta },\phi )\approx \cos \phi .\int \int _{...
...sin \theta -y\cos \theta )\nu _{r}+\nu _{\theta }.\theta )}d\theta \right] dxdy$](img931.png) |
(7.5) |
Comme ce troisième argument ne dépend ni de  , ni de
, ni de  , il n'est
donc pas affecté par le changement de variable que nous avons effectué. Autrement
dit, si je calcule
, il n'est
donc pas affecté par le changement de variable que nous avons effectué. Autrement
dit, si je calcule
 ,
j'obtiens exactement la même expression que 8.5, c'est à dire la
clé de voûte de l'algorithme FORE:
,
j'obtiens exactement la même expression que 8.5, c'est à dire la
clé de voûte de l'algorithme FORE:
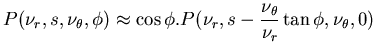 |
(7.6) |
Au vu des angles  utilisés, on peut en première approximation considérer
le cosinus de cet angle comme égal à l'unité. En conséquence, nous pouvons légèrement
simplifier l'Eq.8.6 qui devient:
utilisés, on peut en première approximation considérer
le cosinus de cet angle comme égal à l'unité. En conséquence, nous pouvons légèrement
simplifier l'Eq.8.6 qui devient:
 |
(7.7) |
Cette expression correspond vraiment au coeur de l'algorithme FORE puisqu'elle
nous permet de passer d'une acquisition 3D fournissant un sinogramme à 4 dimensions
(membre de gauche de l'Eq.8.7) en un sinogramme fictif qui
proviendrait d'une acquisition 2D ne comptant donc plus qu'une seule inclinaison
(la variable  est constamment nulle dans le membre de droite de
l'Eq.8.7). Ce sinogramme fictif intègre donc bien les données
issues des différents segments dans des plans transaxiaux. Ces données sont
intégrées à une hauteur particulière (
est constamment nulle dans le membre de droite de
l'Eq.8.7). Ce sinogramme fictif intègre donc bien les données
issues des différents segments dans des plans transaxiaux. Ces données sont
intégrées à une hauteur particulière (
 )
dans le sinogramme fictif. Nous pouvons donc directement en déduire un algorithme.
)
dans le sinogramme fictif. Nous pouvons donc directement en déduire un algorithme.
Elle se traduit par l'utilisation de l'Eq.8.7 dans laquelle
nous cherchons à construire le sinogramme fictif  correspondant
à une acquisition 2D. Lorsqu'il décrit le principe de cet algorithme, Defrise
montre qu'il est nécessaire de considérer différemment certaines régions de
l'espace de Fourier associées à
correspondant
à une acquisition 2D. Lorsqu'il décrit le principe de cet algorithme, Defrise
montre qu'il est nécessaire de considérer différemment certaines régions de
l'espace de Fourier associées à  et
et  . Nous renvoyons le
lecteur à l'article fondateur pour ne conserver que le cas général [29].
L'algorithme correspondant à l'Eq.8.7 est donné Alg.2.
. Nous renvoyons le
lecteur à l'article fondateur pour ne conserver que le cas général [29].
L'algorithme correspondant à l'Eq.8.7 est donné Alg.2.

7.3.2 FOurier Simple Averaging (FOSA).
En reconstruction, du fait du théorème de coupe-tranche, nous savons que les
projections échantillonnent de manière particulière l'espace de Fourier de l'objet
à reconstruire. Ainsi, dès 1981, Stark [87] propose en 2D une reconstruction
qui s'appuie sur ce théorème. L'idée est de prendre la transformation de Fourier
2D des projections
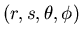 , d'affecter par interpolation
la valeur de chaque fréquence
, d'affecter par interpolation
la valeur de chaque fréquence
 ainsi
obtenue dans la grille de l'espace de Fourier de l'objet
ainsi
obtenue dans la grille de l'espace de Fourier de l'objet
 et de faire la transformée de Fourier 3D inverse pour retrouver l'objet [89,90].
L'inconvénient majeur de cette méthode vient de l'interpolation nécessaire pour
passer des projections à l'espace de Fourier de l'objet. On considère en général,
une grille cartésienne pour tirer parti de la vitesse d'exécution des FFT. L'interpolation
des valeurs sur cette grille conduit à des distorsions de l'image. On trouve
donc différentes méthodes d'interpolation pour passer des projections à la grille
cartésienne: plus proches voisins, bilinéaires, sinus cardinal [75,88,87,94].
D'autres proposent des méthodes par transformation du système de coordonnées
[19]. C'est pourquoi, en nous arrêtant au rebinning nous évitons
ce passage à une grille cartésienne. Autrement dit, on va rebinner les
données dans l'espace de Fourier des projections en affectant les fréquences
et de faire la transformée de Fourier 3D inverse pour retrouver l'objet [89,90].
L'inconvénient majeur de cette méthode vient de l'interpolation nécessaire pour
passer des projections à l'espace de Fourier de l'objet. On considère en général,
une grille cartésienne pour tirer parti de la vitesse d'exécution des FFT. L'interpolation
des valeurs sur cette grille conduit à des distorsions de l'image. On trouve
donc différentes méthodes d'interpolation pour passer des projections à la grille
cartésienne: plus proches voisins, bilinéaires, sinus cardinal [75,88,87,94].
D'autres proposent des méthodes par transformation du système de coordonnées
[19]. C'est pourquoi, en nous arrêtant au rebinning nous évitons
ce passage à une grille cartésienne. Autrement dit, on va rebinner les
données dans l'espace de Fourier des projections en affectant les fréquences
 au niveau des fréquences
au niveau des fréquences
 issues d'un sinogramme ne présentant qu'un seul segment. Les angles
issues d'un sinogramme ne présentant qu'un seul segment. Les angles  restant petits l'interpolation se fait entre 2 grilles voisines.
restant petits l'interpolation se fait entre 2 grilles voisines.
Sur la Fig.8.5.a, les plans de projection  ,
,  ,
, récoltent les photons pour 3 angles de vues différents sous l'inclinaison
récoltent les photons pour 3 angles de vues différents sous l'inclinaison  .
Il s'agit de plans de notre premier segment. Le plan
.
Il s'agit de plans de notre premier segment. Le plan  intègre
les photons sous une inclinaison
intègre
les photons sous une inclinaison
 .
.
Figure 8.5:
Passage des plans de projections dans l'espace de Fourier de l'objet
[Dans l'espace de l'objet.]
![\resizebox*{0,45\textwidth}{!}{\psfrag{Cercle}[][][2]{\( \Omega \)} \psfrag{x}[]...
...\)} \psfrag{PiF4}[][][2]{\( \Pi ^{F}_{4} \)}\includegraphics{imgps/rre_fig5.ps}}](img843.png) [Dans l'espace de Fourier.] [Dans l'espace de Fourier.]
![\resizebox*{0,45\textwidth}{!}{\psfrag{Cercle}[][][2]{\( \Omega \)} \psfrag{x}[]...
...\)} \psfrag{PiF4}[][][2]{\( \Pi ^{F}_{4} \)}\includegraphics{imgps/rre_fig6.ps}}](img844.png)
|
C'est l'information de ce plan que nous allons intégrer dans les plans du premier
segment. Pour cela, prenons la transformée de Fourier 2D suivant les variables
 et
et 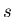 de ces plans de projections. Nous obtenons les transformées
de nos 4 plans de projection
de ces plans de projections. Nous obtenons les transformées
de nos 4 plans de projection
 ,
,
 ,
,
 ,
,
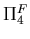 . Du fait du théorème de section centrale, ces derniers échantillonnent
l'espace de Fourier comme sur la Fig.8.5.b. Considérons un point
particulier
. Du fait du théorème de section centrale, ces derniers échantillonnent
l'espace de Fourier comme sur la Fig.8.5.b. Considérons un point
particulier
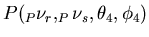 de la
transformée de Fourier 2D
de la
transformée de Fourier 2D
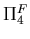 d'un plan de détecteurs incliné.
De manière générale, ce point est ``coincé'' entre les transformées de
deux plans du premier segment. Sur notre figure, il s'agit des plans
d'un plan de détecteurs incliné.
De manière générale, ce point est ``coincé'' entre les transformées de
deux plans du premier segment. Sur notre figure, il s'agit des plans
 et
et
 . Ces plans sont échantillonnés. Le point
. Ces plans sont échantillonnés. Le point  est
donc situé dans un héxaèdre formé par les 8 échantillons fréquentiels les plus
proches de
est
donc situé dans un héxaèdre formé par les 8 échantillons fréquentiels les plus
proches de
 et
et
 (Fig.8.6).
(Fig.8.6).
Figure 8.6:
Interpolation dans l'espace de Fourier.
|
|
On envisage donc l'algorithme (Alg.3) suivant pour rebinner
les données.






Next: 7.4 Ce qu'il faut
Up: 7. Reconstruction et Rebinning.
Previous: 7.2 Dans l'espace de
Contents
Index
Lecomte Jean François
2002-09-07
![]() sur la LOR
sur la LOR
![]() . Nous avons montré que le
plan de projection
. Nous avons montré que le
plan de projection ![]() est invariant par translation suivant le vecteur
est invariant par translation suivant le vecteur
![]() . Le point
. Le point ![]() de projection peut donc être choisi n'importe
où sur la LOR. Par la suite ce point est choisi à mi-chemin entre les deux détecteurs
de projection peut donc être choisi n'importe
où sur la LOR. Par la suite ce point est choisi à mi-chemin entre les deux détecteurs
![]() et
et ![]() . Ceci conduit à des coordonnées faciles à calculer.
. Ceci conduit à des coordonnées faciles à calculer.






![]() (Eq.8.4) comme une
somme vectorielle de complexes
(Eq.8.4) comme une
somme vectorielle de complexes
![]() (Fig.8.3.a). Notons que le changement de signe de
(Fig.8.3.a). Notons que le changement de signe de
![]() fait basculer la phase. Considérons alors les cas suivants:
fait basculer la phase. Considérons alors les cas suivants:
![\resizebox*{0,2\textwidth}{!}{\psfrag{A(theta)}[br][][2]{\( A(\theta ) \)} \psfrag{B(theta)}[][][2]{\( B(\theta ) \)}\includegraphics{imgps/rre_fig8.ps}}](img913.png)
![\resizebox*{0,2\textwidth}{!}{\psfrag{A(theta)}[br][][2]{\( A(\theta ) \)} \psfrag{B(theta)}[][][2]{\( B(\theta ) \)}\includegraphics{imgps/rre_fig9.ps}}](img914.png)
![\resizebox*{0,2\textwidth}{!}{\psfrag{A(theta)}[br][][2]{\( A(\theta ) \)} \psfrag{B(theta)}[][][2]{\( B(\theta ) \)}\includegraphics{imgps/rre_fig10.ps}}](img915.png)
![\resizebox*{0,2\textwidth}{!}{\psfrag{A(theta)}[br][][2]{\( A(\theta ) \)} \psfrag{B(theta)}[][][2]{\( B(\theta ) \)}\includegraphics{imgps/rre_fig11.ps}}](img916.png)





![]() de fréquence
de fréquence
![]() reçoit principalement
des contributions de points situés à une distance
reçoit principalement
des contributions de points situés à une distance
![]() sur les LOR.
sur les LOR.
![]() et en sortant ce terme
de l'intégrale nous obtenons:
et en sortant ce terme
de l'intégrale nous obtenons:
![]() correspondant
à une acquisition 2D. Lorsqu'il décrit le principe de cet algorithme, Defrise
montre qu'il est nécessaire de considérer différemment certaines régions de
l'espace de Fourier associées à
correspondant
à une acquisition 2D. Lorsqu'il décrit le principe de cet algorithme, Defrise
montre qu'il est nécessaire de considérer différemment certaines régions de
l'espace de Fourier associées à ![]() et
et ![]() . Nous renvoyons le
lecteur à l'article fondateur pour ne conserver que le cas général [29].
L'algorithme correspondant à l'Eq.8.7 est donné Alg.2.
. Nous renvoyons le
lecteur à l'article fondateur pour ne conserver que le cas général [29].
L'algorithme correspondant à l'Eq.8.7 est donné Alg.2.

![]() , d'affecter par interpolation
la valeur de chaque fréquence
, d'affecter par interpolation
la valeur de chaque fréquence
![]() ainsi
obtenue dans la grille de l'espace de Fourier de l'objet
ainsi
obtenue dans la grille de l'espace de Fourier de l'objet
![]() et de faire la transformée de Fourier 3D inverse pour retrouver l'objet [89,90].
L'inconvénient majeur de cette méthode vient de l'interpolation nécessaire pour
passer des projections à l'espace de Fourier de l'objet. On considère en général,
une grille cartésienne pour tirer parti de la vitesse d'exécution des FFT. L'interpolation
des valeurs sur cette grille conduit à des distorsions de l'image. On trouve
donc différentes méthodes d'interpolation pour passer des projections à la grille
cartésienne: plus proches voisins, bilinéaires, sinus cardinal [75,88,87,94].
D'autres proposent des méthodes par transformation du système de coordonnées
[19]. C'est pourquoi, en nous arrêtant au rebinning nous évitons
ce passage à une grille cartésienne. Autrement dit, on va rebinner les
données dans l'espace de Fourier des projections en affectant les fréquences
et de faire la transformée de Fourier 3D inverse pour retrouver l'objet [89,90].
L'inconvénient majeur de cette méthode vient de l'interpolation nécessaire pour
passer des projections à l'espace de Fourier de l'objet. On considère en général,
une grille cartésienne pour tirer parti de la vitesse d'exécution des FFT. L'interpolation
des valeurs sur cette grille conduit à des distorsions de l'image. On trouve
donc différentes méthodes d'interpolation pour passer des projections à la grille
cartésienne: plus proches voisins, bilinéaires, sinus cardinal [75,88,87,94].
D'autres proposent des méthodes par transformation du système de coordonnées
[19]. C'est pourquoi, en nous arrêtant au rebinning nous évitons
ce passage à une grille cartésienne. Autrement dit, on va rebinner les
données dans l'espace de Fourier des projections en affectant les fréquences
![]() au niveau des fréquences
au niveau des fréquences
![]() issues d'un sinogramme ne présentant qu'un seul segment. Les angles
issues d'un sinogramme ne présentant qu'un seul segment. Les angles ![]() restant petits l'interpolation se fait entre 2 grilles voisines.
restant petits l'interpolation se fait entre 2 grilles voisines.
![]() ,
, ![]() ,
,![]() récoltent les photons pour 3 angles de vues différents sous l'inclinaison
récoltent les photons pour 3 angles de vues différents sous l'inclinaison ![]() .
Il s'agit de plans de notre premier segment. Le plan
.
Il s'agit de plans de notre premier segment. Le plan ![]() intègre
les photons sous une inclinaison
intègre
les photons sous une inclinaison
![]() .
.
