




Next: 8.4 L'algorithme de reconstruction
Up: 8. Reconstruction Algébrique.
Previous: 8.2 Information a priori
Contents
Index
Nous venons de voir le contexte envisagé pour l'introduction d'information a
priori dans la reconstruction . Or, l'objectif reste néanmoins de reconstruire
une image connaissant ses projections. Il faut donc établir la fonctionnelle
 traduisant la similarité entre des projections calculées en accord
avec un modèle linéaire (Eq.9.1) et les projections vraies issues
de la caméra. Dans ce système:
traduisant la similarité entre des projections calculées en accord
avec un modèle linéaire (Eq.9.1) et les projections vraies issues
de la caméra. Dans ce système:
où le vecteur
 représentatif de l'image correspond au
représentatif de l'image correspond au  composantes
composantes
 de notre image dans la base de représentation choisie. Le vecteur
de notre image dans la base de représentation choisie. Le vecteur
 de dimension
de dimension  représente, quant à lui, les projections
que nous pouvons calculer, partant de notre image
représente, quant à lui, les projections
que nous pouvons calculer, partant de notre image
 , en accord avec
notre modèle linéaire. La matrice
, en accord avec
notre modèle linéaire. La matrice
 traduit la modélisation
de la projection (problème décrit dans la première partie de cette thèse). En
effet,
traduit la modélisation
de la projection (problème décrit dans la première partie de cette thèse). En
effet,  représente la probabilité pour que la composante
représente la probabilité pour que la composante  de l'image soit détectée au niveau du détecteur indexé par
de l'image soit détectée au niveau du détecteur indexé par 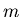 . Cette matrice
se construit grâce à la modélisation du problème direct (nous verrons son implémentation
Ch.10). La fonctionnelle, qui doit nous conduire au choix
d'une image
. Cette matrice
se construit grâce à la modélisation du problème direct (nous verrons son implémentation
Ch.10). La fonctionnelle, qui doit nous conduire au choix
d'une image
 , s'appuie sur la différence existant entre
, s'appuie sur la différence existant entre
 et
et
 .
.
 est donc une fonction de mesure de similarité .
Cette fonction de similarité dépend du modèle de bruit envisagé. Nous allons
maintenant uniquement décrire la reconstruction algébrique s'appuyant sur un
bruit de nature gaussienne. Ce modèle conduit à une mesure de similarité basée
sur la distance. Même si elles existent, des mesures de similarités plus exotiques,
comme celle basée sur l'entropie [5], ne sont pas décrites ici.
Il existe encore à ce niveau de multiples degrés de liberté. Nous donnons également
en Annexe (Ch:B) l'approche basée sur le modèle poissonnien.
Ce modèle conduit à un algorithme de reconstruction OSEM-OSL
décrit dans le même chapitre.
est donc une fonction de mesure de similarité .
Cette fonction de similarité dépend du modèle de bruit envisagé. Nous allons
maintenant uniquement décrire la reconstruction algébrique s'appuyant sur un
bruit de nature gaussienne. Ce modèle conduit à une mesure de similarité basée
sur la distance. Même si elles existent, des mesures de similarités plus exotiques,
comme celle basée sur l'entropie [5], ne sont pas décrites ici.
Il existe encore à ce niveau de multiples degrés de liberté. Nous donnons également
en Annexe (Ch:B) l'approche basée sur le modèle poissonnien.
Ce modèle conduit à un algorithme de reconstruction OSEM-OSL
décrit dans le même chapitre.
Attardons nous sur le modèle gaussien. . On pose que
les projections réelles
 correspondent aux projections calculées
correspondent aux projections calculées
 corrompues par un bruit additif gaussien
corrompues par un bruit additif gaussien
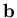 de matrice de variance-covariance
de matrice de variance-covariance
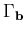 dépendante des
projections:
dépendante des
projections:
La fonction de similarité revient alors à mesurer la distance entre les projections
calculées et réelles.
Si on considère la distance pondérée par la matrice de variance-covariance du
bruit, on obtient une mesure de similarité basée sur la distance de Mahalanobis.
où 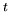 traduit la transposée. Pour réduire le champ d'investigation
et faciliter le calcul de la distance, on peut ensuite faire des hypothèses
sur la nature du bruit et plus précisément sur la matrice de variance-covariance.
Fessler [34] envisage une matrice
traduit la transposée. Pour réduire le champ d'investigation
et faciliter le calcul de la distance, on peut ensuite faire des hypothèses
sur la nature du bruit et plus précisément sur la matrice de variance-covariance.
Fessler [34] envisage une matrice
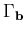 qui
est diagonale et dont les éléments diagonaux
qui
est diagonale et dont les éléments diagonaux
 représentent les variances attachées aux projections
représentent les variances attachées aux projections  . Il donne
dans son article l'expression pour le calcul de ces variances. Dans le cas où
tous les
. Il donne
dans son article l'expression pour le calcul de ces variances. Dans le cas où
tous les
 sont égaux à
sont égaux à
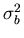 ,
le bruit additif est considéré comme blanc et la distance de Mahalanobis devient
une simple distance euclidienne:
,
le bruit additif est considéré comme blanc et la distance de Mahalanobis devient
une simple distance euclidienne:





Next: 8.4 L'algorithme de reconstruction
Up: 8. Reconstruction Algébrique.
Previous: 8.2 Information a priori
Contents
Index
Lecomte Jean François
2002-09-07
![]() traduisant la similarité entre des projections calculées en accord
avec un modèle linéaire (Eq.9.1) et les projections vraies issues
de la caméra. Dans ce système:
traduisant la similarité entre des projections calculées en accord
avec un modèle linéaire (Eq.9.1) et les projections vraies issues
de la caméra. Dans ce système:
![]() correspondent aux projections calculées
correspondent aux projections calculées
![]() corrompues par un bruit additif gaussien
corrompues par un bruit additif gaussien
![]() de matrice de variance-covariance
de matrice de variance-covariance
![]() dépendante des
projections:
dépendante des
projections:

