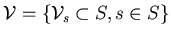 doit vérifier les deux conditions suivantes:
doit vérifier les deux conditions suivantes:
Nous allons considérer les images comme un ensemble de régions homogènes séparées par des bords francs. C'est pourquoi, nous envisageons la régularisation dans une approche markovienne. En effet, les champs markoviens sont bien adaptés à cette hypothèse. Nous rappelons brièvement certaines notions relatives aux champs markoviens dont nous aurons besoin.. Cette description, bien connue actuellement, s'appuie sur les travaux fondateurs de S. et D. Geman [38].
Dans l'approche statistique, l'image
![]() correspond à un champ aléatoire,
de sorte qu'on peut associer la probabilité
correspond à un champ aléatoire,
de sorte qu'on peut associer la probabilité
![]() d'obtenir cette
image. Chaque élément
d'obtenir cette
image. Chaque élément ![]() , ou voxel, est localisé en un site
, ou voxel, est localisé en un site ![]() (sa valeur est prise dans l'espace des états
(sa valeur est prise dans l'espace des états
![]() ). L'ensemble
des sites
). L'ensemble
des sites ![]() représente une grille qui correspond,
dans notre cas, au centre de chaque voxel. Le voisinage
représente une grille qui correspond,
dans notre cas, au centre de chaque voxel. Le voisinage
![]() associe
à tout site
associe
à tout site ![]() de la grille
de la grille ![]() , une série de sites
, une série de sites ![]() de cette
même grille (ses voisins). Le système de voisinage
de cette
même grille (ses voisins). Le système de voisinage
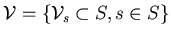 doit vérifier les deux conditions suivantes:
doit vérifier les deux conditions suivantes:
Le voxel n'est pas voisin avec lui même. Et si le voxel ![]() du
site
du
site ![]() est voisin du voxel
est voisin du voxel ![]() au site
au site ![]() , alors
, alors ![]() est aussi voisin de
est aussi voisin de ![]() (réciprocité du voisinage). D'autre part,
pour un site
(réciprocité du voisinage). D'autre part,
pour un site ![]() , il peut être utile de vouloir énoncer tous ses voisins.
Cela se fait par l'utilisation d'une clique. Une clique
, il peut être utile de vouloir énoncer tous ses voisins.
Cela se fait par l'utilisation d'une clique. Une clique
![]() , c'est d'abord le site
, c'est d'abord le site ![]() considéré puis le sous ensemble des
sites de
considéré puis le sous ensemble des
sites de ![]() qui lui sont voisins 2 à 2. Toutes les cliques que l'on peut
construire sur la grille
qui lui sont voisins 2 à 2. Toutes les cliques que l'on peut
construire sur la grille ![]() forment l'ensemble des cliques
forment l'ensemble des cliques
![]() :
:
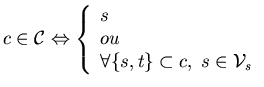
On dit que
![]() est un champ de Markov par rapport au système de voisinage
est un champ de Markov par rapport au système de voisinage
![]() si l'image vérifie, pour tout
si l'image vérifie, pour tout ![]() :
:
La deuxième propriété revient à dire que la connaissance du voisinage
Derrière ces définitions mathématiques se retrouvent des notions facilement
palpables. En effet, il ne faut pas oublier que notre vecteur
![]() représente
une distribution de radioactivité. Il y a de grandes chances pour que cette
distribution soit relativement lisse. Deux zones proches dans l'espace auront
une activité ``voisine''. De surcroît, un forte augmentation locale se
traduira également par une augmentation dans une région périphérique. Autrement
dit, les voxels sont spatialement corrélés. Cette notion de proximité, de corrélation,
se traduit aisément à l'aide d'un voisinage basé sur la distance entre deux
voxels. Deux voxels sont voisins si la distance qui les sépare est inférieure
à une valeur seuil. Cette distance fixe l'ordre du voisinage. La notion de champ
de Markov nous dit que les répercussions d'un site sont confinées à son voisinage.
La probabilité en un site, n'est pas fonction de tous les autres voxels mais
seulement des sites voisins. Dans le cas où on considère le voisinage associé
à la distance entre voxels, le fait qu'un voxel ait une valeur
représente
une distribution de radioactivité. Il y a de grandes chances pour que cette
distribution soit relativement lisse. Deux zones proches dans l'espace auront
une activité ``voisine''. De surcroît, un forte augmentation locale se
traduira également par une augmentation dans une région périphérique. Autrement
dit, les voxels sont spatialement corrélés. Cette notion de proximité, de corrélation,
se traduit aisément à l'aide d'un voisinage basé sur la distance entre deux
voxels. Deux voxels sont voisins si la distance qui les sépare est inférieure
à une valeur seuil. Cette distance fixe l'ordre du voisinage. La notion de champ
de Markov nous dit que les répercussions d'un site sont confinées à son voisinage.
La probabilité en un site, n'est pas fonction de tous les autres voxels mais
seulement des sites voisins. Dans le cas où on considère le voisinage associé
à la distance entre voxels, le fait qu'un voxel ait une valeur ![]() ne dépend en termes statistiques que de l'état des voxels
ne dépend en termes statistiques que de l'état des voxels ![]() qui
sont proches du voxel
qui
sont proches du voxel ![]() (
(
![]() ). Le voisinage
basé sur la distance est certainement le plus courant et conduit à un voisinage
dont la forme est la même quel que soit le site ou voxel considéré (aux bords
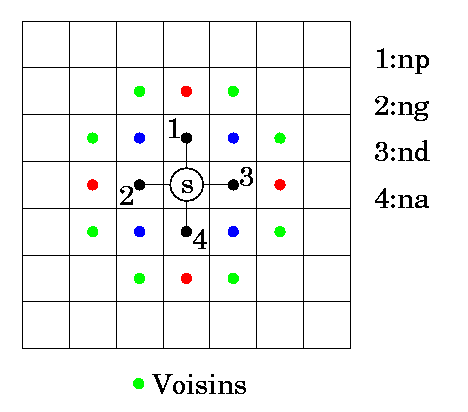
du volume près). On en donne une représentation Fig.9.2. Les
ronds correspondent à des voisins du site
). Le voisinage
basé sur la distance est certainement le plus courant et conduit à un voisinage
dont la forme est la même quel que soit le site ou voxel considéré (aux bords
du volume près). On en donne une représentation Fig.9.2. Les
ronds correspondent à des voisins du site ![]() . En fonction de la distance
à ce site, une couleur indique l'ordre du voisinage considéré. Un voisinage
basé sur 4-connexité correspond à un voisinage d'ordre 1, la 8-connexité à un
voisinage d'ordre 2.
. En fonction de la distance
à ce site, une couleur indique l'ordre du voisinage considéré. Un voisinage
basé sur 4-connexité correspond à un voisinage d'ordre 1, la 8-connexité à un
voisinage d'ordre 2.
|
Notons, qu'un tel voisinage exclut la corrélation entre des zones éloignées dans l'objet. Par exemple, si nous savons a priori que deux régions cérébrales distantes sont corrélées de manière fonctionnelle, le voisinage construit sur la distance n'en tiendra pas compte8.1 . Pour intégrer cette information au niveau de notre reconstruction (ce qui est possible), il faudrait définir un voisinage utilisant des informations fonctionnelles qui ne sont pas uniquement basées sur la proximité. Il faudrait définir un voisinage dédié.
La propriété de localité Eq.9.4 nous donne des indications
sur les propriétés statistiques de manière ponctuelle. Or, nous cherchons à
caractériser la probabilité globale
![]() . Le lien entre ces
deux grandeurs nous est fourni par le théorème de Hammersley-Clifford.
. Le lien entre ces
deux grandeurs nous est fourni par le théorème de Hammersley-Clifford.
Ce théorème nous dit :
Théorème I : Hammersley-Clifford
Si
![]() est markovien sur la grille
est markovien sur la grille ![]() avec le système de voisinage
choisi
avec le système de voisinage
choisi
![]() , alors la probabilité d'observer
, alors la probabilité d'observer
![]() suit
une distribution de Gibbs relativement à
suit
une distribution de Gibbs relativement à
![]() .
Cette distribution est de la forme:
.
Cette distribution est de la forme:
![$\displaystyle I\! \! P(\mathbf{f})=\frac{1}{Z}exp\left[ -\sum _{c\in \mathcal{C}}U_{c}(\mathbf{f})\right] $](img995.png)
Cette expression correspond à une distribution connue en physique statistique.
Chaque valeur ![]() correspond à un état énergétique. Chaque image correspond
donc à une configuration énergétique précise où chaque voxel est dans un état
énergétique particulier. La somme
correspond à un état énergétique. Chaque image correspond
donc à une configuration énergétique précise où chaque voxel est dans un état
énergétique particulier. La somme
![]() traduit l'énergie associée
à cette configuration. La localité nous dit que cette fonction d'énergie globale
est en fait la somme des énergies locales pour chacun des sites (le potentiel
d'interaction
traduit l'énergie associée
à cette configuration. La localité nous dit que cette fonction d'énergie globale
est en fait la somme des énergies locales pour chacun des sites (le potentiel
d'interaction ![]() est défini pour une clique qui correspond à l'énumération
des voisins en un site). Nous voyons également
que l'image la plus probable est celle qui rendra
est défini pour une clique qui correspond à l'énumération
des voisins en un site). Nous voyons également
que l'image la plus probable est celle qui rendra ![]() minimale. Toujours
par analogie avec la physique, cela veut dire que la configuration la plus stable
est celle d'énergie minimale.
minimale. Toujours
par analogie avec la physique, cela veut dire que la configuration la plus stable
est celle d'énergie minimale.
Le potentiel d'interaction ![]() est donc une fonction construite sur
une clique
est donc une fonction construite sur
une clique ![]() . Plaçons nous en un site
. Plaçons nous en un site ![]() , la clique
, la clique ![]() construite
sur ce site nous donne des voisins (des sites) qui interagissent avec
construite
sur ce site nous donne des voisins (des sites) qui interagissent avec ![]() .
Si nous prenons deux images différentes mais dont les valeurs en chacun des
sites définis par cette clique
.
Si nous prenons deux images différentes mais dont les valeurs en chacun des
sites définis par cette clique ![]() sont égales, alors les potentiels d'interactions
calculés sur chacune de ces deux images seront égaux:
sont égales, alors les potentiels d'interactions
calculés sur chacune de ces deux images seront égaux:
On dispose ainsi d'un nouveau degré de liberté. Une fois que le système de voisinage
est fixé, il est encore nécessaire de choisir le mode d'interactions entre les
voisins. Le choix du potentiel d'interaction est fonction du but recherché.
Fréquemment, en segmentation, on travaille avec un modèle d'Ising ou un modèle
de Potts à p niveaux. Dans notre cas, nous avons dans l'esprit de régulariser
(de lisser), on va donc introduire une fonction de potentiel construite sur
un opérateur différentiel. Si on prend deux sites ![]() et
et ![]() d'une
clique
d'une
clique ![]() , le potentiel d'interaction sera lié à l'opérateur différentiel
d'ordre
, le potentiel d'interaction sera lié à l'opérateur différentiel
d'ordre ![]() :
:
![]() . En fonction de l'ordre, cet
opérateur agit soit sur l'image elle même (ordre 0), soit sur l'approximation
discrète de la dérivée première (ordre 1) ou seconde (ordre 2). L'énergie est
alors [39]:
. En fonction de l'ordre, cet
opérateur agit soit sur l'image elle même (ordre 0), soit sur l'approximation
discrète de la dérivée première (ordre 1) ou seconde (ordre 2). L'énergie est
alors [39]:

Tout ceci est bien général. Notre but n'est pas de faire une description aussi exhaustive que possible, mais juste de sensibiliser en montrant la richesse et la souplesse du modèle. Nous allons donc maintenant restreindre et illustrer le modèle retenu.
On ne considère que l'opérateur différentiel d'ordre 1 (![]() ) et
le système de voisinage
) et
le système de voisinage
![]() basé sur la distance. Dans une image
basé sur la distance. Dans une image
![]() , envisageons un voxel (site
, envisageons un voxel (site ![]() particulier
particulier
![]() .
Il nous faut, dans un premier temps, définir ses voisins. Pour l'illustration,
nous choisissons une 6-connexité. Nous avons, en plus du
site
.
Il nous faut, dans un premier temps, définir ses voisins. Pour l'illustration,
nous choisissons une 6-connexité. Nous avons, en plus du
site ![]() , 6 voisins qui sont
, 6 voisins qui sont
![]() .
A ces sites voisins correspondent respectivement les valeurs dans le volume
.
A ces sites voisins correspondent respectivement les valeurs dans le volume
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Dans un deuxième temps, il faut construire pour ce site ![]() , le potentiel
d'interaction associé à chaque clique
, le potentiel
d'interaction associé à chaque clique ![]() . De manière discrète, l'opérateur
différentiel d'ordre 1 se traduit juste par une différence entre les valeurs
de deux voisins (
. De manière discrète, l'opérateur
différentiel d'ordre 1 se traduit juste par une différence entre les valeurs
de deux voisins (
![]() ). Nous obtenons
donc directement le potentiel d'interaction pour la clique construite au voxel
). Nous obtenons
donc directement le potentiel d'interaction pour la clique construite au voxel
![]() :
:
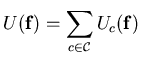 |
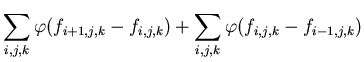 |
||
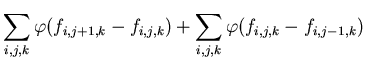 |
|||
 |
Il est clair que
![]() , l'énergie totale correspond donc
à notre fonctionnelle
, l'énergie totale correspond donc
à notre fonctionnelle
![]() . Dans cette optique, la régularisation
consiste à chercher l'image présentant le minimum d'énergie. Insistons encore
sur le fait que l'énergie envisagée repose déjà sur deux hypothèses :
. Dans cette optique, la régularisation
consiste à chercher l'image présentant le minimum d'énergie. Insistons encore
sur le fait que l'énergie envisagée repose déjà sur deux hypothèses :
Pour expliciter la régularisation et donc la prise en compte des discontinuités,
nous prenons l'approche de Charbonnier [17]. Dans cette approche,
notre but est de trouver les propriétés que doit suivre la fonction de potentiel
![]() pour préserver les discontinuités dans notre image en partant
du fait que nous devons rendre le critère
pour préserver les discontinuités dans notre image en partant
du fait que nous devons rendre le critère ![]() minimal. Nous replacerons
ensuite les conditions obtenues dans le contexte des processus de lignes.
minimal. Nous replacerons
ensuite les conditions obtenues dans le contexte des processus de lignes.
Avant d'aller plus loin, explicitons de nouvelles hypothèses:
Nous avons vu que pour minimiser ![]() , nous devions minimiser la somme
des énergies
, nous devions minimiser la somme
des énergies
![]() en chaque site
en chaque site
![]() . Plaçons
nous en un site particulier et minimisons localement. Supposons que nous sommes
en 2D, nous avons donc une image
. Plaçons
nous en un site particulier et minimisons localement. Supposons que nous sommes
en 2D, nous avons donc une image
![]() . Si on
suppose un voisinage basé sur une 4-connexité, nous avons
pour chaque site, 4 voisins
. Si on
suppose un voisinage basé sur une 4-connexité, nous avons
pour chaque site, 4 voisins
![]() qui sont impliqués pour le système de voisinage considéré (Fig.9.2).
La minimisation locale du critère s'écrit donc:
qui sont impliqués pour le système de voisinage considéré (Fig.9.2).
La minimisation locale du critère s'écrit donc:
![$\displaystyle \Delta _{pond}(f_{n_{s}})\leftrightarrow \left[ \begin{array}{ccc...
...a _{n_{t}}} & \lambda _{n_{d}}\\
0 & \lambda _{n_{a}} & 0
\end{array}\right] $](img1044.png)
Supposons maintenant que tous les coefficients sont égaux à 1 (
![]() ),
alors ce Laplacien pondéré devient:
),
alors ce Laplacien pondéré devient:
![$\displaystyle \Delta _{pond}(f_{n_{s}})\leftrightarrow \left[ \begin{array}{ccc}
0 & 1 & 0\\
1 & -4 & 1\\
0 & 1 & 0
\end{array}\right] $](img1046.png)
![$\displaystyle \Delta _{pond}(f_{n_{s}})\leftrightarrow \left[ \begin{array}{ccc}
0 & 1 & 0\\
0 & -3 & 1\\
0 & 1 & 0
\end{array}\right] $](img1049.png)
En résumé, on constate que pour lisser dans des zones homogènes, il nous faut des coefficients proches de 1. Pour préserver une discontinuité, et donc casser l'opération de lissage, il faut que le coefficient soit nul pour cette direction .
Cette approche, nous permet aisément de comprendre les conditions imposées,
non sur la fonction de potentiel
![]() , mais sur la fonction de
pondération
, mais sur la fonction de
pondération
![]() .
Nous venons de voir les conditions aux limites. en rajoutant comme contrainte
pour la fonction de pondération le fait qu'elle doit varier de manière continue
entre ses limites, nous aboutissons aux conditions suivantes:
.
Nous venons de voir les conditions aux limites. en rajoutant comme contrainte
pour la fonction de pondération le fait qu'elle doit varier de manière continue
entre ses limites, nous aboutissons aux conditions suivantes:
Pour lisser tout en préservant les discontinuités, la fonction de potentiel
![]() mais surtout la fonction de pondération utilisée doit vérifier
les conditions suivantes [17]:
mais surtout la fonction de pondération utilisée doit vérifier
les conditions suivantes [17]:
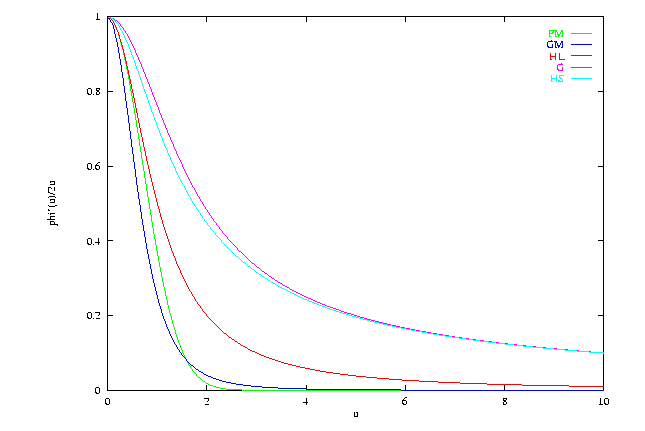
Si on consulte la littérature pour retrouver les fonctions de potentiels qui
furent utilisées pour lisser des volumes, on constate que les scientifiques
ne manquent pas d'imagination. Les approches diffèrent et conduisent parfois
à des conditions contradictoires sur les fonctions de potentiel ([54]
versus [39]). Bien souvent, la recherche est empirique [53,42].
Dans le tableau Tab.9.1,nous donnons quelques unes des fonctions
les plus utilisées dans la littérature en précisant celles susceptibles de préserver
les discontinuités en accord avec le critère que nous avons retenu.
|
|
Après avoir choisi le voisinage, travaillant avec l'opérateur différentiel du
premier ordre avec la fonction de potentiel retenue, on cherche à minimiser
le critère ![]() :
:


On construit une nouvelle fonction d'énergie
![]() qui, bien que définie sur un domaine plus étendu (
qui, bien que définie sur un domaine plus étendu (
![]() et
et
![]() ),
a le même minimum global que
),
a le même minimum global que
![]() en
en
![]() . Elle peut être
manipulée par des méthodes d'algèbre linéaire.
. Elle peut être
manipulée par des méthodes d'algèbre linéaire.
On introduit donc une variable auxiliaire
![]() qui va rendre le critère
qui va rendre le critère
![]() plus facile à manipuler. On remplace le critère:
plus facile à manipuler. On remplace le critère:
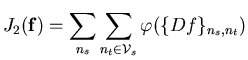

Théorème II : Geman & Reynolds étendu
Soit une fonction ![]() définie de
définie de
![]() qui vérifie:
qui vérifie:
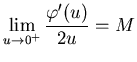 |
|||
 |
|||
 |
|||
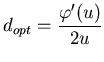
De par ce théorème, si nous posons
![]() ,
nous arrivons à montrer que le critère étendu
,
nous arrivons à montrer que le critère étendu ![]() et le critère
classique
et le critère
classique ![]() sont égaux pour une valeur de
sont égaux pour une valeur de
![]() précise.
précise.
Arrêtons nous sur les conditions de ce théorème. Si ![]() et
et ![]() alors ces conditions sont équivalentes à celles posées sur la fonction de potentiel
Eq.9.6. En effet, il y a équivalence entre la concavité
d'une fonction et la stricte décroissance de sa dérivée. Or, la dérivée de
alors ces conditions sont équivalentes à celles posées sur la fonction de potentiel
Eq.9.6. En effet, il y a équivalence entre la concavité
d'une fonction et la stricte décroissance de sa dérivée. Or, la dérivée de
![]() est justement la fonction de pondération.
est justement la fonction de pondération.
En choisissant une fonction de potentiel vérifiant les conditions Eq.9.6,
nous pouvons construire une fonction étendue
![]() . Cette
fonction nous permet de construire un nouveau critère
. Cette
fonction nous permet de construire un nouveau critère ![]() étendu
présentant le même minimum en
étendu
présentant le même minimum en
![]() que
que ![]() . Qui plus est :
. Qui plus est :
Dans un article fondateur, les frères Geman proposaient déjà en 1984 [38]
d'introduire une variable auxiliaire
![]() . De booléenne en 1984, elle
devient continue et trouve sa justification en 1992 (Théorème de Geman&Reynolds
[39]). Cette variable, appelée processus de ligne,
sert à marquer les discontinuités. Ce processus de ligne est localisé sur une
grille
. De booléenne en 1984, elle
devient continue et trouve sa justification en 1992 (Théorème de Geman&Reynolds
[39]). Cette variable, appelée processus de ligne,
sert à marquer les discontinuités. Ce processus de ligne est localisé sur une
grille ![]() duale à la grille de l'image
duale à la grille de l'image ![]() .
. ![]() correspond
à une grille de sites interstitiels ou sites contours On trouve une illustration
de ces grilles Fig.9.4.
correspond
à une grille de sites interstitiels ou sites contours On trouve une illustration
de ces grilles Fig.9.4.
 |
 |
La notion de processus de ligne est bien utile car elle permet de mieux sentir
la signification de la variable auxiliaire. En effet, pour le système de voisinage
basé sur la distance, pour un potentiel d'interaction basé sur l'opérateur différentiel
de premier ordre (gradient discret) et pour une fonction de potentiel répondant
au théorème de Geman & Reynolds étendu, cette variable auxiliaire
![]() peut être vue comme correspondant aux images transformées par la fonction de
pondération des images de gradient . En 2D, pour une 4-connexité, nous obtenons
2 images représentant le processus de ligne: une,
peut être vue comme correspondant aux images transformées par la fonction de
pondération des images de gradient . En 2D, pour une 4-connexité, nous obtenons
2 images représentant le processus de ligne: une,
![]() , suivant la
direction associé à
, suivant la
direction associé à ![]() et l'autre
et l'autre
![]() suivant l'axe des
suivant l'axe des ![]() (Fig.9.5) obtenu à partir de
(Fig.9.5) obtenu à partir de
![]() par:
par: