8.4 L'algorithme de reconstruction : MAP-GCSQ.

Nous venons d'établir totalement la fonctionnelle $J(\mathbf{f})$ à minimiser pour reconstruire une image partant de ses projections. Il s'agit maintenant de choisir un algorithme pour effectuer cette minimisation. Là encore, le choix est vaste. Rappelons cette contrainte: nous voulons minimiser la fonctionnelle $J(\mathbf{f})$ par l'utilisation d'un algorithme déterministe. Cela nous a déjà permis de réduire le choix de la fonction de potentiel. Si nous souhaitons utiliser un tel algorithme, c'est surtout du fait de sa rapidité d'exécution par rapport aux algorithmes stochastiques.

Nous laissons donc de côté les algorithmes de recuit simulé (échantillonneur de Gibbs par exemple [38]). Les méthodes stochastiques sont lourdes, car elles nécessitent de nombreux tirages aléatoires. Besag propose une version déterministe de ces méthodes de recuit simulé par une réactualisation locale des sites (ICM pour Iterated Conditional Mode), mal adaptée à notre cas. Nous envisageons donc pour minimiser notre fonctionnelle une méthode de descente.

8.4.1 Stratégie de minimisation.

Rappelons d'abord que le choix que nous avons fait sur la fonction de potentiel, nous a permis de construire un critère $J^{*}_{2}(\mathbf{f},\mathbf{d})$ étendu pour la régularisation. De ce choix découle le critère MAP que nous envisageons de minimiser:

$$J(\mathbf{f}) = J_{1}(\mathbf{f})+\beta ^{2}J_{2}(\mathbf{f})$$

$$\Downarrow$$

$$J^{*}(\mathbf{f}) = J_{1}(\mathbf{f})+\beta ^{2}J^{*}_{2}(\mathbf{f},\mathbf{d})$$

La constante $\beta$, que nous rajoutons, nous permet de contrôler le poids de la régularisation ($J_{2}$) vis à vis de l'importance accordée aux données ($J_{1}$). Le critère $J_{2}$ est délicat car il n'est pas quadratique. Il ne conduit donc pas, lors de la minimisation, à des équations linéaires en $\mathbf{f}$. Du fait des propriétés du critère étendu $J^{*}_{2}$(Par.9.2.4.5), Charbonnier propose de minimiser par étapes une suite de critères plus faciles à manipuler [17]. Les critères à minimiser sont définis en fixant alternativement la valeur de la variable principale $\mathbf{f}$, puis celle de la variable auxiliaire $\mathbf{d}$. Nous obtenons le schéma de minimisation décrit Alg.4.

Dans un contexte de régularisation semi-quadratique, et pour une fonction de potentiel vérifiant les conditions Eq.9.6, la première étape du processus itéré ne pose pas de problème. En effet, nous avons une expression littérale des discontinuités lorsque $\mathbf{f}$ est fixé (Par.9.2.4.5. et Eq.9.7.):

$$\mathbf{d}=\frac{\varphi '(\mathbf{Df})}{2\mathbf{Df}}$$

Pour la deuxième étape, lorsque $\mathbf{d}$ est fixé, le critère devient quadratique en $\mathbf{f}$ et peut être minimisé par des méthodes classiques d'algèbre linéaire. Il reste à en choisir une !

8.4.2 Equations normales du système.

Nous voulons minimiser la fonctionnelle $J(\mathbf{f})$ alors que les discontinuités $\mathbf{d}$ sont fixées. Plaçons nous, pour commencer, dans le cas d'un critère d'attache aux données le plus général possible basé sur la distance de Mahalanobis, nous avons:

$$J(\mathbf{f})=(\mathbf{p}-\hat{\mathbf{p}})^{t}\Gamma ^{-1}_{\mat... ...}})+\sum _{n_{s}}\sum _{n_{t}\in \mathcal{V}_{s}}\varphi (\{Df\}_{n_{s},n_{t}})$$

Nous minimisons par rapport à $\mathbf{f}$:

$$\frac{\delta J(\mathbf{f})}{\delta \mathbf{f}}=2\mathbf{H}^{t}\Ga... ...^{t}\Gamma ^{-1}_{\mathbf{b}}\mathbf{p}-2\Delta _{pond}(\mathbf{f})\mathbf{f}=0$$ (8.8)

Comme au Par.9.2.4.5., dans l'expression Eq.9.8, le terme $\Delta _{pond}(\mathbf{f})$ nous pose problème. Or, les coefficients de ce Laplacien pondéré sont calculés à partir de la fonction de pondération et donc des valeurs de discontinuités $\mathbf{d}$ (Par.9.2.4.2). Du fait de l'emploi d'un algorithme de minimisation alternée (Alg.4.), ces discontinuités ont été estimées à l'étape 1 de l'algorithme. Nous avons donc une valeur fixe de $\Delta _{pond}(\mathbf{f})=\Delta _{pond}\vert _{\mathbf{d}}$ calculée à partir de ce jeu fixe de discontinuités. Nous pouvons donc dans l'Eq.9.8 regrouper les termes relatifs à $\mathbf{f}$ en considérant $\Delta _{pond}$ comme indépendant de $\mathbf{f}$.

$$(\mathbf{H}^{t}\Gamma ^{-1}_{\mathbf{b}}\mathbf{H}-\Delta _{pond}\vert _{\mathbf{d}})\mathbf{f} = \mathbf{H}^{t}\Gamma ^{-1}_{\mathbf{b}}\mathbf{p}$$

$$\mathbf{A}\mathbf{f} = \mathbf{c}$$ (8.9)

Nous faisons apparaître un nouveau système linéaire $\mathbf{A}\mathbf{f}=\mathbf{c}$ qu'il nous faut résoudre pour obtenir notre image $\mathbf{f}$.

La matrice $\mathbf{A}$ est une matrice carrée de dimension $[N,N]$, $\mathbf{f}$ et $\mathbf{c}$ sont des vecteurs de dimensions $[N,1]$. Pour une image standard en TEP, nous avons $N=128\times 128\times 63=1032192$ voxels. La matrice $\mathbf{A}$ est donc de dimensions impressionnantes puisqu'elle compte quelque $10^{12}$ termes. Même avec un CRAY à sa disposition, l'inversion directe de la matrice par une méthode de type factorisation SVD ou QR est donc compromise. En 2D, ce type de méthode a pu être envisagé [85,13,56]. Mais les puissances de calculs disponibles actuellement ferment la route à ce type de méthode dans un cas tridimensionnel (surtout si on conserve les matrices dans leur intégralité, ce que l'on fait rarement en pratique puisque la matrice est très creuse). On va donc utiliser une méthode itérative de résolution qui va construire une série d'images $\mathbf{f}_{\alpha }$ telles que:

$$\mathbf{f}_{\alpha +1}=\mathbf{f}_{\alpha }+\lambda _{\alpha }\mathbf{k}_{\alpha }$$

où $\lambda _{\alpha }$ est un terme de relaxation (vectoriel ou matriciel) et $\mathbf{k}_{\alpha }$ le terme de correction apporté d'une itération à l'autre. Evidemment, on s'arrange pour que cette série d'images converge vers une solution qui correspond à un minimum du MAP. Ce minimum est global si la fonction de pondération est convexe, et local autrement.

Il faut dire que même pour un minimum global, la solution obtenue ne sera pas forcément conforme à ce que nous attendons réellement! En effet bien des fois la solution mathématique n'est pas la réponse pertinente!

Les méthodes itératives constituant encore un ensemble trop vaste, on se restreint aux seules méthodes dites de descente. Et même au sein de ces méthodes de descente, seule la méthode de gradient conjugué est envisagée. Notre choix a été guidé par l'étude comparative de nombreuses méthodes itératives de reconstruction effectuée par Koulibaly [52]. Nous laissons donc de coté: les méthodes de type Gauss-Seidel ou de sur-relaxations successives (SOR pour Successiv Over Relaxation) [79], les méthodes ILST (Iterativ Least Square Solution) [92], ART (Algebraic Reconstruction Technic) [43], les méthodes de descente par plus grande pente (steepest descent), la méthode de Newton ou Quasi-Newton.

8.4.3 La méthode de gradient conjugué (GC).

8.4.3.1 Principe.

Supposons que nous partions d'une estimée initiale de notre image $\mathbf{f}$ (vecteur de dimension $[N,1]$) et dans cet espace de dimension $N$, nous fixons une direction de descente $\mathbf{k}$ (vecteur de dimension $[N,1]$). Alors toute fonction $\psi (\mathbf{f})$ construite sur $\mathbf{f}$ peut être minimisée suivant cette direction. On peut donc rêver qu'une succession de minimisation suivant des directions différentes va nous conduire à notre minimum. Les différentes méthodes de descente vont donc différer sur la façon dont les directions successives de minimisation sont choisies et sur la façon dont le minimum est choisi suivant chaque direction. Supposons que nous ayons choisi une méthode pour minimiser suivant une direction, alors une itération peut se résumer comme ceci:

Partant d'une image $\mathbf{f}$ et d'une direction $\mathbf{k}$, pour la fonction $\psi$, il faut trouver le scalaire $\lambda$ (pas de descente) qui minimise $\psi (\mathbf{f}+\lambda \mathbf{k}).$ On remplace $\mathbf{f}$ par $\mathbf{f}+\lambda \mathbf{k}.$ On change de direction $\mathbf{k}$ et on recommence.

Si nous définissons la fonction $\psi (\mathbf{f})=\frac{1}{2}\mathbf{f}^{t}\mathbf{A}\mathbf{f}-\mathbf{f}^{t}\mathbf{c}$, en cherchant son minimum ( $\frac{\delta \psi (\mathbf{f})}{\delta \mathbf{f}}=\mathbf{A}\mathbf{f}-\mathbf{c}=0$), nous retombons sur le système linéaire (Eq.9.9). Autrement dit, résoudre le système Eq.9.9 est équivalent à minimiser la fonction $\psi$.

8.4.3.2 Pas de descente.

Notre résolution est itérative, au bout de $\alpha -1$ itérations, nous avons déterminé $\alpha -1$ directions de projections $\{\mathbf{k}_{i}\}_{i=1,\alpha -1}$, l'image à laquelle nous sommes parvenus est donc:

$$\mathbf{f}_{\alpha -1}=\sum _{i=1}^{\alpha -1}y_{i}\mathbf{k}_{i}=\mathbf{K}_{\alpha -1}\mathbf{y}$$

Nous effectuons une itération de plus alors:

$$\mathbf{f}_{\alpha }=\mathbf{f}_{\alpha -1}+\lambda \mathbf{k}_{\alpha }$$

Nous voulons que cette nouvelle itération minimise notre fonction $\psi$, exprimons la valeur de cette fonctionnelle pour cette itération:

$$\psi (\mathbf{f}_{\alpha })=\psi (\mathbf{K}_{\alpha -1}\mathbf{y... ... }^{t}\mathbf{A}\mathbf{k}_{\alpha }-\lambda \mathbf{k}^{t}_{\alpha }\mathbf{c}$$ (8.10)

Dans cette expression, le terme $\lambda \mathbf{y}^{t}\mathbf{K}^{t}_{\alpha -1}\mathbf{A}\mathbf{k}_{\alpha }$ nous pose problème. En effet, s'il n'existait pas, nous pourrions diviser Eq.9.10 en deux termes : un dépendant uniquement des $\alpha -1$ itérations précédentes et un ne dépendant que de l'itération courante. Le terme nous gène, il suffit donc de le supprimer en l'annulant. Rien de plus simple, il suffit de prendre la direction de projection de l'itération $\alpha$ A-conjuguée par rapport aux $\alpha -1$ itérations précédentes. C'est à dire:

$$\forall i<\alpha ,\; \mathbf{k}^{t}_{i}\mathbf{A}\mathbf{k}_{\alpha }=0\Leftrightarrow \mathbf{K}^{t}_{\alpha -1}\mathbf{A}\mathbf{k}_{\alpha }=0$$

Nous pouvons alors séparer la minimisation Eq.9.10 en deux :

$$\min _{\mathbf{y},\lambda }\psi (\mathbf{f}_{\alpha })=\min _{\ma... ...f{K}_{\alpha -1}\mathbf{y})+\min _{\lambda }\psi (\lambda \mathbf{k}_{\alpha })$$

On suppose évidemment que les $\alpha -1$ itérations n'ont pas été faites au hasard et donc que l'image $\mathbf{f}_{\alpha -1}=\mathbf{K}_{\alpha -1}\mathbf{y}$ minimise le premier terme de cette expression. Pour minimiser le deuxième terme, il suffit de choisir:

$$\lambda _{\alpha }=\frac{\mathbf{k}_{\alpha }^{t}\mathbf{c}}{\mat... ...\mathbf{r}_{\alpha -1}}{\mathbf{k}^{t}_{\alpha }\mathbf{A}\mathbf{k}_{\alpha }}$$

où $\mathbf{r}_{\alpha }=\mathbf{A}\mathbf{f}_{\alpha }-\mathbf{c}$ désigne le résidu lié à l'itération $\alpha$^8.4. Notre pas de descente optimal $\lambda _{\alpha }$ dans une direction $\mathbf{k}_{\alpha }$ est donc connu.

8.4.3.3 Direction de descente.

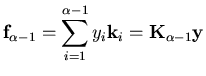
Il nous reste maintenant à définir comment choisir à chaque itération la direction de descente optimale. On peut montrer [40] qu'une solution optimale visant à réduire le résidu consiste à choisir la direction de descente $\mathbf{k}_{\alpha }$ qui s'appuie sur la direction de descente précédente $\mathbf{k}_{\alpha -1}$ et sur le résidu de l'itération $\mathbf{r}_{\alpha }$. Plus précisément:

$$\mathbf{k}_{\alpha }=\mathbf{r}_{\alpha }+\kappa _{\alpha }\mathbf{k}_{\alpha -1}$$

En utilisant le fait que les directions $\mathbf{k}_{\alpha }$ et $\mathbf{k}_{\alpha -1}$ doivent être A-conjuguées, on trouve la valeur du scalaire :

$$\kappa _{\alpha }=\frac{\vert\vert\mathbf{r}_{\alpha }\vert\vert^{2}}{\vert\vert\mathbf{r}_{\alpha -1}\vert\vert^{2}}$$

En mettant tous ces éléments bout à bout, on arrive à l'algorithme de Gradient conjugué utilisé qui conserve l'esprit de l'algorithme tel qu'il est décrit par Hestenes et Stiefel [44,40].

8.4.4 Algorithme de reconstruction.

En regroupant l'algorithme de minimisation alternée (Alg.4) d'une part et l'algorithme de gradient conjugué (Alg.5) d'autre part, nous aboutissons à la méthode de reconstruction algébrique implémentée. Elle est illustrée Alg.6