




Next: 5.4 Confrontation du Modèle
Up: 5. Bruit dans le
Previous: 5.2 Hypothèses.
Contents
Index
Subsections
Le modèle de bruit que nous avons retenu comporte principalement deux constantes
 et
et 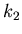 . Pour bruiter un sinogramme calculé à l'aide de
ce modèle, il est impératif de choisir ces constantes de manière judicieuse,
pour que les propriétés des sinogrammes de bruit calculés
. Pour bruiter un sinogramme calculé à l'aide de
ce modèle, il est impératif de choisir ces constantes de manière judicieuse,
pour que les propriétés des sinogrammes de bruit calculés  et
réels
et
réels  soient les plus proches possibles. On va procéder au
choix de ces constante de manière séquentielle, en estimant d'abord
soient les plus proches possibles. On va procéder au
choix de ces constante de manière séquentielle, en estimant d'abord  puis
puis 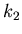 .
.
Pour estimer  , on va chercher à minimiser la distance euclidienne
entre les projections vraies
, on va chercher à minimiser la distance euclidienne
entre les projections vraies
 et la projection analytique
et la projection analytique
 , autrement dit
, autrement dit
En effet,
Nous obtenons donc pour le produit scalaire défini par :
Ceci conduit tout simplement en développant à choisir :
Suivant une écriture vectorielle, cette expression devient:
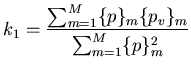 |
(5.3) |
Pour le modèle de bruit choisi, nous pouvons calculer un sinogramme de bruit
par la différence entre les projections idéales et les projections d'un volume
bruité normalisé.
Nous voulons que les propriétés statistiques de ce bruit  se
rapprochent le plus possible de celles du sinogramme de bruit calculé par la
différence entre les projections idéales et les projections issues d'un examen
réel.
se
rapprochent le plus possible de celles du sinogramme de bruit calculé par la
différence entre les projections idéales et les projections issues d'un examen
réel.
Le sinogramme  se déduit du bruit
se déduit du bruit  sur le volume
servant de fantôme par une série d'opérations linéaires. Comme le bruit
sur le volume
servant de fantôme par une série d'opérations linéaires. Comme le bruit  est de nature gaussienne, le sinogramme suit également une loi gaussienne. Pour
caractériser le bruit sur les projections, il est donc nécessaire de définir
les premiers moments de la fonction aléatoire
est de nature gaussienne, le sinogramme suit également une loi gaussienne. Pour
caractériser le bruit sur les projections, il est donc nécessaire de définir
les premiers moments de la fonction aléatoire  .
.
Pour cela, il suffit de calculer
![$ I\! \! E[b^{p}_{b}] $](img522.png) où
où  traduit l'espérance. En utilisant la définition Eq.6.4, nous obtenons:
traduit l'espérance. En utilisant la définition Eq.6.4, nous obtenons:
Or, d'après les hypothèses faites sur le bruit
![$ I\! \! E[b_{n}(x,y)]=0 $](img524.png) (Eq.6.1),
nous avons donc finalement :
Le sinogramme de bruit est centré.
(Eq.6.1),
nous avons donc finalement :
Le sinogramme de bruit est centré.
A ce niveau, nous introduisons la fonction d'autocorrélation du bruit
 qui, comme le sinogramme de bruit est centré se réduit à:
qui, comme le sinogramme de bruit est centré se réduit à:
Du fait de la définition du sinogramme de bruit calculé (Eq.6.4),
nous obtenons pour l'autocorrélation:
Nous avons Eq.6.1, l'expression de la variance du bruit, cela nous
conduit à:
La variance du sinogramme de bruit est alors simplement donnée par:
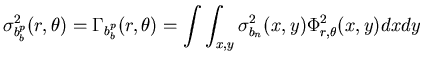 |
(5.6) |
La définition de la fonction caractéristique  nous permet d'écrire
simplement
nous permet d'écrire
simplement
 , et comme
de plus,
, et comme
de plus,
 ,
l'Eq.6.6 devient:
,
l'Eq.6.6 devient:
 |
(5.7) |
En résumé, les deux premiers moments du bruit sont:
![$\displaystyle \left\{ \begin{array}{ll} I\! \! E\left[ b^{p}_{b}(r,\theta )\rig...
...}_{b}(r,\theta )\right] & =k_{1}k^{2}_{2}\times p(r,\theta ) \end{array}\right.$](img538.png) |
(5.8) |
5.3.2.4 Remarque sur l'autocorrélation.
Le calcul effectué au paragraphe 6.3.2.3 n'est pas qu'un exercice
de style, il permet de justifier à lui seul l'hypothèse (Par.6.2.2)
qui nous conduit à bruiter le volume d'émission plutôt que le sinogramme obtenu
par la projection de ce volume.
Restons dans le cas bidimensionnel et supposons que chaque couple de détecteurs
(de largeur  ) référencé par
) référencé par
 ne ``voit'' que
les photons situés dans une bande de largeur
ne ``voit'' que
les photons situés dans une bande de largeur  (Fig. 6.1).
La fonction
(Fig. 6.1).
La fonction
 vaut donc 1 uniquement si le pixel
vaut donc 1 uniquement si le pixel
 est compris dans cette bande.
est compris dans cette bande.
Supposons d'abord que la variance du bruit sur le volume d'émission soit indépendante
de la position  . Dans ce cas, et malheureusement seulement dans
ce cas, il devient possible de sortir la variance du bruit de l'intégrale dans
l'expression de la fonction d'autocorrélation. De ce fait, en posant
. Dans ce cas, et malheureusement seulement dans
ce cas, il devient possible de sortir la variance du bruit de l'intégrale dans
l'expression de la fonction d'autocorrélation. De ce fait, en posant
 ,
on obtient:
,
on obtient:
'intégration restante
 correspond
à la surface définie par l'intersection des deux fonctions caractéristiques
correspond
à la surface définie par l'intersection des deux fonctions caractéristiques
 et
et
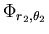 . Dans notre
exemple bidimensionnel, la corrélation suivant la première variable
. Dans notre
exemple bidimensionnel, la corrélation suivant la première variable  est triviale. Les bandes de détection sont disjointes, la corrélation pour
est triviale. Les bandes de détection sont disjointes, la corrélation pour
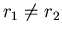 est donc nulle. Intéressons nous plutôt à la corrélation suivant la deuxième
variable, ou corrélation suivant l'angle de vue
est donc nulle. Intéressons nous plutôt à la corrélation suivant la deuxième
variable, ou corrélation suivant l'angle de vue  . Le calcul de
la surface d'intersection est relativement simple. On désigne par
. Le calcul de
la surface d'intersection est relativement simple. On désigne par
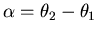 la différence angulaire entre 2 vues. Sur la figure Fig.6.1
la différence angulaire entre 2 vues. Sur la figure Fig.6.1
Figure:
Corrélation entre les vues.
|
, pour une différence angulaire suffisamment grande, la surface d'intersection
est égale à  . On trouve dans ce cas que
. On trouve dans ce cas que
 .
De fait la fonction d'autocorrélation est définie par:
Pour des angles
.
De fait la fonction d'autocorrélation est définie par:
Pour des angles  petits et proches de 0, cette expression de
la fonction d'autocorrélation tend vers l'infini. En fait, pour cela il faudrait
que les bandes sur lesquelles sont intégrés les photons soient infiniment longues.
Or, ce n'est pas le cas, elles sont limitées au diamètre
petits et proches de 0, cette expression de
la fonction d'autocorrélation tend vers l'infini. En fait, pour cela il faudrait
que les bandes sur lesquelles sont intégrés les photons soient infiniment longues.
Or, ce n'est pas le cas, elles sont limitées au diamètre  d'une couronne
de détecteurs. De fait, la fonction d'autocorrélation est bornée en 0.
On représente Fig.6.2, le comportement de cette fonction d'autocorrélation
pour une différence angulaire suffisamment grande.
d'une couronne
de détecteurs. De fait, la fonction d'autocorrélation est bornée en 0.
On représente Fig.6.2, le comportement de cette fonction d'autocorrélation
pour une différence angulaire suffisamment grande.
Figure:
Profil d'autocorrélation calculé
|
|
Pour vérifier ce calcul, nous allons prendre 2 fantômes correspondant à 2 volumes
géométriquement différents:
- un parallélépipède (Volume
 ) de dimensions
) de dimensions
 voxels de
voxels de
 , d'amplitude
, d'amplitude  ,
situé dans un coin du volume.
,
situé dans un coin du volume.
- un ellipsoïde (Volume
 ) de dimensions
) de dimensions
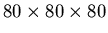 voxels de
voxels de
 , d'amplitude
, d'amplitude  situé au centre du volume.
situé au centre du volume.
Ces volumes originaux vont être bruités par l'addition d'un bruit blanc gaussien
dont l'écart type est indépendant du signal présent dans le volume. On effectue
pour chaque voxel de chaque volume, un tirage aléatoire. Les voxels du fond
ne présentant pas de signal sont également bruités. Partant des volumes non
bruités, on calcule les sinogrammes  et
et  à partir des
volumes bruités, on calcule les sinogrammes
à partir des
volumes bruités, on calcule les sinogrammes  et
et  .
Cela nous permet, par différence, d'estimer les sinogrammes de bruit
.
Cela nous permet, par différence, d'estimer les sinogrammes de bruit
 et
et
 . Sur le premier segment de ces sinogrammes de bruit,
on va déterminer le profil d'autocorrélation au centre du sinogramme suivant
les angles de vues
. Sur le premier segment de ces sinogrammes de bruit,
on va déterminer le profil d'autocorrélation au centre du sinogramme suivant
les angles de vues  (mesure globale par l'utilisation des FFT).
Les profils correspondant à chacun de ces 2 cas sont illustrés Fig.6.3.
(mesure globale par l'utilisation des FFT).
Les profils correspondant à chacun de ces 2 cas sont illustrés Fig.6.3.
Figure:
Autocorrélation avec un bruit additif gaussien indépendant du signal

|

|
|
[Parallélépipède]
|
[Ellipsoïde]
|
Sur ces figures, il faut d'abord constater que les profils d'autocorrélation
ont une forme semblable à celui obtenu lors du calcul théorique (Fig.6.2).
D'autre part, et c'est là le point essentiel, les profils sont identiques pour
chacun des deux volumes. En effet, dans le cas d'un bruit indépendant du signal,
nous avons montré que la corrélation entre les vues était uniquement liée à
la géométrie d'acquisition. Or cette dernière est la même pour le calcul des
projections des deux volumes.
Malheureusement pour nous, la statistique d'émission est de nature poissonnienne
où, comme nous l'avons supposé, gaussienne dépendante du signal dans le volume.
Il n'est donc plus possible de sortir
 de l'intégrale
Eq.6.5. Cette dernière n'étant pas indépendante de la position
de l'intégrale
Eq.6.5. Cette dernière n'étant pas indépendante de la position
 . Reprenons alors nos deux volumes
. Reprenons alors nos deux volumes  et
et  non bruités. Cette fois ci, pour obtenir les volumes bruités
non bruités. Cette fois ci, pour obtenir les volumes bruités  et
et  , nous effectuons un tirage poissonnien en chaque voxel.
Ainsi, seuls les voxels non nuls (ceux du parallélépipède pour
, nous effectuons un tirage poissonnien en chaque voxel.
Ainsi, seuls les voxels non nuls (ceux du parallélépipède pour  et ceux de l'ellipsoïde pour
et ceux de l'ellipsoïde pour  ) sont bruités. Le fond reste
nul. Nous procédons comme précédemment pour obtenir les deux sinogrammes de
bruit
) sont bruités. Le fond reste
nul. Nous procédons comme précédemment pour obtenir les deux sinogrammes de
bruit
 et
et
 et nous calculons les profils
d'autocorrélation suivant les angles de vues (Fig.6.4).
et nous calculons les profils
d'autocorrélation suivant les angles de vues (Fig.6.4).
Figure:
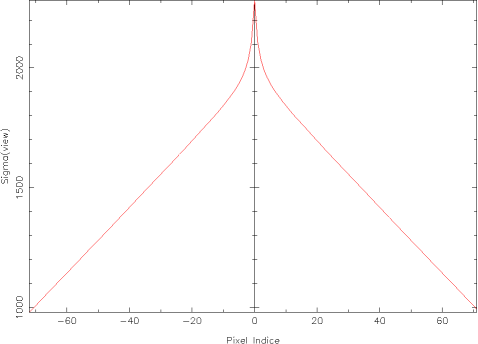
Autocorrélation avec un bruit additif gaussien dépendant du signal
|

|
|
[Parallélépipède]
|
[Ellipsoïde]
|
Nous constatons, dans ce cas, des profils nettement différents. Plus le volume
est grand (la taille de l'ellipsoïde est plus grande que celle du parallélépipède),
plus le profil d'autocorrélation rejoint celui obtenu pour un bruit indépendant
du signal (le profil d'autocorrélation du bruit pour l'ellipsoïde donné
Fig.6.4.b ressemble plus au profil théorique que celui du parallélépipède
donné Fig.6.4.a).
Ainsi, la projection induit, sur le sinogramme de bruit, une variabilité
sur la corrélation qui est fonction non seulement de la géométrie d'acquisition
mais également de l'objet à imager.
Cela exclut la possibilité de modéliser le bruit directement sur les projections
et explique le choix que nous avons fait de bruiter les volumes avant la projection.





Next: 5.4 Confrontation du Modèle
Up: 5. Bruit dans le
Previous: 5.2 Hypothèses.
Contents
Index
Lecomte Jean François
2002-09-07
![]() et
et ![]() . Pour bruiter un sinogramme calculé à l'aide de
ce modèle, il est impératif de choisir ces constantes de manière judicieuse,
pour que les propriétés des sinogrammes de bruit calculés
. Pour bruiter un sinogramme calculé à l'aide de
ce modèle, il est impératif de choisir ces constantes de manière judicieuse,
pour que les propriétés des sinogrammes de bruit calculés ![]() et
réels
et
réels ![]() soient les plus proches possibles. On va procéder au
choix de ces constante de manière séquentielle, en estimant d'abord
soient les plus proches possibles. On va procéder au
choix de ces constante de manière séquentielle, en estimant d'abord ![]() puis
puis ![]() .
.
![]() , on va chercher à minimiser la distance euclidienne
entre les projections vraies
, on va chercher à minimiser la distance euclidienne
entre les projections vraies
![]() et la projection analytique
et la projection analytique
![]() , autrement dit
, autrement dit
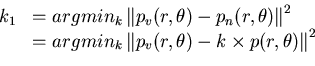



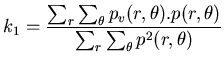
![]() se
rapprochent le plus possible de celles du sinogramme de bruit calculé par la
différence entre les projections idéales et les projections issues d'un examen
réel.
se
rapprochent le plus possible de celles du sinogramme de bruit calculé par la
différence entre les projections idéales et les projections issues d'un examen
réel.
![]() se déduit du bruit
se déduit du bruit ![]() sur le volume
servant de fantôme par une série d'opérations linéaires. Comme le bruit
sur le volume
servant de fantôme par une série d'opérations linéaires. Comme le bruit ![]() est de nature gaussienne, le sinogramme suit également une loi gaussienne. Pour
caractériser le bruit sur les projections, il est donc nécessaire de définir
les premiers moments de la fonction aléatoire
est de nature gaussienne, le sinogramme suit également une loi gaussienne. Pour
caractériser le bruit sur les projections, il est donc nécessaire de définir
les premiers moments de la fonction aléatoire ![]() .
.
![]() où
où ![]() traduit l'espérance. En utilisant la définition Eq.6.4, nous obtenons:
traduit l'espérance. En utilisant la définition Eq.6.4, nous obtenons:
![$\displaystyle I\! \! E[b^{p}_{b}]=\int \int _{x,y}I\! \! E[b_{n}(x,y)]\Phi _{r,\theta }(x,y)dxdy$](img523.png)
![]() qui, comme le sinogramme de bruit est centré se réduit à:
qui, comme le sinogramme de bruit est centré se réduit à:
![$\displaystyle I\! \! E\left[ \int \int _{x,y}b_{n}(x,y)\Phi _{r_{1},\theta _{1}...
...)dxdy\times \int \int _{u,v}b_{n}(u,v)\Phi _{r_{2},\theta _{2}}(u,v)dudv\right]$](img529.png)
![$\displaystyle I\! \! E\left[ \int \int _{x,y}\int \int _{u,v}b_{n}(x,y)b_{n}(u,v)\Phi _{r_{1},\theta _{1}}(x,y)\Phi _{r_{2},\theta _{2}}(u,v)dxdydudv\right]$](img530.png)
![$\displaystyle \int \int _{x,y}\int \int _{u,v}I\! \! E\left[ b_{n}(x,y)b_{n}(u,v)\right] \Phi _{r_{1},\theta _{1}}(x,y)\Phi _{r_{2},\theta _{2}}(u,v)dxdydudv$](img531.png)
![]() ) référencé par
) référencé par
![]() ne ``voit'' que
les photons situés dans une bande de largeur
ne ``voit'' que
les photons situés dans une bande de largeur ![]() (Fig. 6.1).
La fonction
(Fig. 6.1).
La fonction
![]() vaut donc 1 uniquement si le pixel
vaut donc 1 uniquement si le pixel
![]() est compris dans cette bande.
est compris dans cette bande.
![]() . Dans ce cas, et malheureusement seulement dans
ce cas, il devient possible de sortir la variance du bruit de l'intégrale dans
l'expression de la fonction d'autocorrélation. De ce fait, en posant
. Dans ce cas, et malheureusement seulement dans
ce cas, il devient possible de sortir la variance du bruit de l'intégrale dans
l'expression de la fonction d'autocorrélation. De ce fait, en posant
![]() ,
on obtient:
,
on obtient:




![]() de l'intégrale
Eq.6.5. Cette dernière n'étant pas indépendante de la position
de l'intégrale
Eq.6.5. Cette dernière n'étant pas indépendante de la position
![]() . Reprenons alors nos deux volumes
. Reprenons alors nos deux volumes ![]() et
et ![]() non bruités. Cette fois ci, pour obtenir les volumes bruités
non bruités. Cette fois ci, pour obtenir les volumes bruités ![]() et
et ![]() , nous effectuons un tirage poissonnien en chaque voxel.
Ainsi, seuls les voxels non nuls (ceux du parallélépipède pour
, nous effectuons un tirage poissonnien en chaque voxel.
Ainsi, seuls les voxels non nuls (ceux du parallélépipède pour ![]() et ceux de l'ellipsoïde pour
et ceux de l'ellipsoïde pour ![]() ) sont bruités. Le fond reste
nul. Nous procédons comme précédemment pour obtenir les deux sinogrammes de
bruit
) sont bruités. Le fond reste
nul. Nous procédons comme précédemment pour obtenir les deux sinogrammes de
bruit
![]() et
et
![]() et nous calculons les profils
d'autocorrélation suivant les angles de vues (Fig.6.4).
et nous calculons les profils
d'autocorrélation suivant les angles de vues (Fig.6.4).

