




Next: 5.5 Filtrage.
Up: 5. Bruit dans le
Previous: 5.3 Estimation des constantes.
Contents
Index
Subsections
Nous disposons maintenant de tous les éléments pour construire un sinogramme
de manière analytique. Il reste à confronter ce modèle avec un sinogramme réel
issu d'une acquisition afin d'en estimer les paramètre  et
et 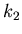 .
.
Pour cela, nous avons utilisé le fantôme d'Hoffman 3D
disponible à CYCERON. Ce fantôme est un cylindre en plexiglas contenant 19 tranches
évidées afin de recevoir un liquide radioactif (Fig.6.5)
Figure:
Fantôme Hoffman 3D
|
|
. La forme de chacune des découpes se rapproche de celle observé dans des coupes
axiales de cerveau. Chacune des tranches fait 6.09 mm d'épaisseur. Afin de n'utiliser
qu'un seul liquide radioactif pour remplir le fantôme, chacune de ces tranches
est subdivisée en 5 sous-tranches (2 de 0.762mm et 3 de 1.524mm). Cette subdivision
permet en remplissant le fantôme d'obtenir 2 niveaux de radioactivité pour différencier
la substance blanche (SB) de la substance grise (SG) dans un ratio
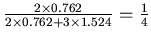 .
Ce ratio est en accord avec le ratio des activités biochimiques de chacune de
ces deux substances. Le fantôme a une capacité d'environ 1150
.
Ce ratio est en accord avec le ratio des activités biochimiques de chacune de
ces deux substances. Le fantôme a une capacité d'environ 1150  .
Pour réaliser un examen, on produit une solution aqueuse contenant du Fluor
radioactif. On remplit ce cylindre avec cette substance en ayant au préalable
ajouté un solvant pour que la solution se répartisse uniformément à l'intérieur
du cylindre. La solution contient
.
Pour réaliser un examen, on produit une solution aqueuse contenant du Fluor
radioactif. On remplit ce cylindre avec cette substance en ayant au préalable
ajouté un solvant pour que la solution se répartisse uniformément à l'intérieur
du cylindre. La solution contient
 mCi de Fluor. Le fantôme
ayant été agité afin d'uniformiser la répartition de la radioactivité, nous
commençons l'acquisition 22 minutes après la création de notre traceur fluoré.
Pour ce fantôme, nous allons réaliser 10 acquisitions (10 Frames).
Les 5 premières frames enregistrent chacune 130 Millions (M) de coups.
Il s'agit des évènements vrais, les fortuits ayant été supprimés de manière
dynamique durant l'acquisition. Les 5 dernières frames ne comportent
que 20 M de coups. On attend que le fantôme ne soit plus radioactif pour lancer
une transmission. Des études ont montré que le nombre de coups minimum d'un
examen de transmission donnant une correction d'atténuation correcte est de
130M. Dans notre cas, 260M de coups ont été acquis pour réaliser la transmission.
Par un jeu de sommation de frames , on obtient une série de sinogrammes
indépendants couvrant une large gamme de nombre de coups. Ces sinogrammes sont
ensuite corrigés à l'aide des outils disponibles sur la caméra ECAT HR+. Nous
obtenons ainsi une série de 10 sinogrammes (Tab.6.1)
mCi de Fluor. Le fantôme
ayant été agité afin d'uniformiser la répartition de la radioactivité, nous
commençons l'acquisition 22 minutes après la création de notre traceur fluoré.
Pour ce fantôme, nous allons réaliser 10 acquisitions (10 Frames).
Les 5 premières frames enregistrent chacune 130 Millions (M) de coups.
Il s'agit des évènements vrais, les fortuits ayant été supprimés de manière
dynamique durant l'acquisition. Les 5 dernières frames ne comportent
que 20 M de coups. On attend que le fantôme ne soit plus radioactif pour lancer
une transmission. Des études ont montré que le nombre de coups minimum d'un
examen de transmission donnant une correction d'atténuation correcte est de
130M. Dans notre cas, 260M de coups ont été acquis pour réaliser la transmission.
Par un jeu de sommation de frames , on obtient une série de sinogrammes
indépendants couvrant une large gamme de nombre de coups. Ces sinogrammes sont
ensuite corrigés à l'aide des outils disponibles sur la caméra ECAT HR+. Nous
obtenons ainsi une série de 10 sinogrammes (Tab.6.1)
prêts à être reconstruits.
Nous disposons également d'une version numérique du fantôme. Il s'agit d'un
volume  qui présente deux classes pour chacune des 2 substances
(
qui présente deux classes pour chacune des 2 substances
( et
et  ) présentant respectivement
) présentant respectivement  et
et  voxels. Les valeurs de chacune de ces deux substances sont dans le ratio
voxels. Les valeurs de chacune de ces deux substances sont dans le ratio
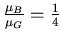 ,
où
,
où  représente la valeur moyenne sur la classe considérée. Seul le
ratio nous importe puisque c'est par la détermination de la constante
représente la valeur moyenne sur la classe considérée. Seul le
ratio nous importe puisque c'est par la détermination de la constante  (Par.6.3.1)
que nous normalisons les projections calculées et donc notre volume par rapport
aux projections vraies. Cependant la valeur de la constante
(Par.6.3.1)
que nous normalisons les projections calculées et donc notre volume par rapport
aux projections vraies. Cependant la valeur de la constante  est
liée aux valeurs affectées à chacune des deux classes. Si je choisis un fantôme
d'activité double pour la projection, la constante
est
liée aux valeurs affectées à chacune des deux classes. Si je choisis un fantôme
d'activité double pour la projection, la constante  sera divisée
par deux. C'est pourquoi par la suite les valeurs des constantes
sera divisée
par deux. C'est pourquoi par la suite les valeurs des constantes  seront données pour des valeurs du fantômes choisies en accord avec Tab.6.2.
seront données pour des valeurs du fantômes choisies en accord avec Tab.6.2.
Table:
Valeurs du fantôme.
|
|
Ce volume a une dimension  , où chaque plan (indice
, où chaque plan (indice  )
correspond à une des tranches du fantôme de Hoffman. A l'aide d'un sinogramme
de Tab.6.1 de bonne qualité (i.e. présentant un grand nombre de
coups), nous effectuons une reconstruction par rétroprojection filtrée (voir
partie sur reconstruction). Nous obtenons ainsi un volume de
)
correspond à une des tranches du fantôme de Hoffman. A l'aide d'un sinogramme
de Tab.6.1 de bonne qualité (i.e. présentant un grand nombre de
coups), nous effectuons une reconstruction par rétroprojection filtrée (voir
partie sur reconstruction). Nous obtenons ainsi un volume de
 voxels de dimensions
voxels de dimensions
 . Nous allons
ensuite recaler notre fantôme numérique
. Nous allons
ensuite recaler notre fantôme numérique  sur ce volume reconstruit
afin de le positionner dans le référentiel de la caméra comme l'était le fantôme
physique. Ce recalage nous permet aussi d'ajuster les dimensions des voxels
de notre fantôme numérique. En effet, pour effectuer ce recalage nous utilisons
l'algorithme AIR développé par R. Woods [100,99]. Cet algorithme
nous permet d'ajuster 9 paramètres pour recaler le fantôme numérique dans l'espace
de la caméra (3 rotations, 3 translations, 3 homothéties). C'est ce fantôme
recalé
sur ce volume reconstruit
afin de le positionner dans le référentiel de la caméra comme l'était le fantôme
physique. Ce recalage nous permet aussi d'ajuster les dimensions des voxels
de notre fantôme numérique. En effet, pour effectuer ce recalage nous utilisons
l'algorithme AIR développé par R. Woods [100,99]. Cet algorithme
nous permet d'ajuster 9 paramètres pour recaler le fantôme numérique dans l'espace
de la caméra (3 rotations, 3 translations, 3 homothéties). C'est ce fantôme
recalé  qui nous servira de base pour la création de sinogrammes simulés.
qui nous servira de base pour la création de sinogrammes simulés.
Le fait de recaler le fantôme va induire des interpolations dans le volume (rotations
et homothéties notamment). C'est pourquoi, même si le fantôme comporte intrinsèquement
toujours 2 classes, il présentera par endroits des valeurs différentes de 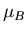 et
et  . Nous allons donc définir une notion de région
. Nous allons donc définir une notion de région  [16].
Un voxel
[16].
Un voxel  5.3 de l'image est considéré comme appartenant à la région
5.3 de l'image est considéré comme appartenant à la région  si sa valeur
si sa valeur
![$ \{f\}_{n}\in [\mu _{R}-\Delta _{R},\mu _{R}+\Delta _{R}] $](img595.png) et si un certain
nombre de voxels de son voisinage sont dans le même intervalle de valeurs.
et si un certain
nombre de voxels de son voisinage sont dans le même intervalle de valeurs.
 représente une certaine tolérance par rapport à la moyenne. De ce fait, il est
nécessaire en plus de la moyenne
représente une certaine tolérance par rapport à la moyenne. De ce fait, il est
nécessaire en plus de la moyenne  sur la région de définir la variance
sur la région de définir la variance
 sur cette région. Les valeurs pour le fantôme recalé sont consignées
dans les tableau Tab.6.3.
sur cette région. Les valeurs pour le fantôme recalé sont consignées
dans les tableau Tab.6.3.
A l'aide d'un des sinogrammes issu de Tab.6.1 d'une part et du
fantôme numérique recalé, nous pouvons construire les sinogrammes de bruit  et
et  . La démarche pour les obtenir est illustrée Fig.6.6
. La démarche pour les obtenir est illustrée Fig.6.6
Figure 6.6:
Principe de construction des sinogrammes de bruit.
|
|
. La projection analytique de  (fantôme normalisé) nous fournit
le sinogramme idéal
(fantôme normalisé) nous fournit
le sinogramme idéal 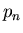 qui nous servira de référence. Pour construire
le sinogramme de bruit, nous bruitons
qui nous servira de référence. Pour construire
le sinogramme de bruit, nous bruitons  en accord avec Par.6.2.2.
Ce fantôme bruité est projeté pour obtenir un sinogramme bruité
en accord avec Par.6.2.2.
Ce fantôme bruité est projeté pour obtenir un sinogramme bruité  .
Nous pouvons maintenant construire nos sinogrammes de bruits comme définis Par.6.3.2.1.
.
Nous pouvons maintenant construire nos sinogrammes de bruits comme définis Par.6.3.2.1.
A titre de première illustration, nous allons déterminer les constantes  et
et 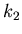 pour un des sinogrammes de Tab.6.1. Nous allons
le faire pour le sinogramme présentant 260 M de coups (
pour un des sinogrammes de Tab.6.1. Nous allons
le faire pour le sinogramme présentant 260 M de coups ( ). La
détermination de la constante
). La
détermination de la constante  ne pose aucun problème, elle s'obtient
directement grâce à Eq.6.3. Il faut noter toutefois que cette valeur
de constante est totalement dépendante des valeurs présentes dans le fantôme.
Cette constante est relative au fantôme décrit dans Tab.6.3.
La détermination de la constante
ne pose aucun problème, elle s'obtient
directement grâce à Eq.6.3. Il faut noter toutefois que cette valeur
de constante est totalement dépendante des valeurs présentes dans le fantôme.
Cette constante est relative au fantôme décrit dans Tab.6.3.
La détermination de la constante 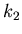 pose plus de problèmes. Nous allons
donc la déterminer graphiquement. Pour différentes valeurs de cette constante,
on calcule 10 plans de projections du sinogramme de bruit
pose plus de problèmes. Nous allons
donc la déterminer graphiquement. Pour différentes valeurs de cette constante,
on calcule 10 plans de projections du sinogramme de bruit
 .
Ces plans
.
Ces plans
 correspondent à 10 directions de projections
contenues dans le plan transaxial (10 valeurs de
correspondent à 10 directions de projections
contenues dans le plan transaxial (10 valeurs de  pour
pour  ).
Nous obtenons
).
Nous obtenons
 valeurs du sinogramme de
bruit
valeurs du sinogramme de
bruit
 à comparer aux
à comparer aux  valeurs de
valeurs de  prises pour les mêmes plans. Pour la comparaison, nous allons d'abord normaliser
chacune de ces deux portions de sinogramme. D'après l'Eq.6.8,
nous avons sur le sinogramme de bruit un bruit gaussien de variance en 3D égale
à
prises pour les mêmes plans. Pour la comparaison, nous allons d'abord normaliser
chacune de ces deux portions de sinogramme. D'après l'Eq.6.8,
nous avons sur le sinogramme de bruit un bruit gaussien de variance en 3D égale
à
 |
(5.9) |
On normalise donc les deux portions de sinogrammes en divisant chacun des  termes par
termes par
 . Les bruits obtenus
devraient donc, en théorie suivre chacun une loi normale.
. Les bruits obtenus
devraient donc, en théorie suivre chacun une loi normale.
5.4.2.1 Critère du
 .
.
Pour comparer les sinogrammes de bruit empiriques et calculés par un test du
 , il est nécessaire de déterminer les histogrammes. Ces deux
histogrammes comportent chacun
, il est nécessaire de déterminer les histogrammes. Ces deux
histogrammes comportent chacun  classes. Le nombre de classes est
fonction du nombre d'échantillons choisis dans les sinogrammes de bruit et donc
de
classes. Le nombre de classes est
fonction du nombre d'échantillons choisis dans les sinogrammes de bruit et donc
de  . La similarité entre ces deux histogrammes est alors mesurée
par le critère
. La similarité entre ces deux histogrammes est alors mesurée
par le critère  défini par:
défini par:
où
 représente le nombre de dexels du sinogramme
de bruit
représente le nombre de dexels du sinogramme
de bruit  qui sont comptés dans la classe
qui sont comptés dans la classe  .5.4 Pour chaque valeur de la constante
.5.4 Pour chaque valeur de la constante 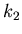 une valeur de ce critère
une valeur de ce critère  peut être calculée. En traçant
peut être calculée. En traçant
 , nous cherchons sur
la courbe la valeur de
, nous cherchons sur
la courbe la valeur de 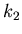 minimisant le critère
minimisant le critère  .
Pour le sinogramme
.
Pour le sinogramme  , nous obtenons les résultats illustrés Fig.6.7.
, nous obtenons les résultats illustrés Fig.6.7.
Figure 6.7:
Courbe
 pour le sinogramme
pour le sinogramme
 .
.
|
|
Il est facile sur cette courbe de déterminer la valeur optimale pour la variable
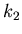 . Les valeurs optimales pour les deux constantes
. Les valeurs optimales pour les deux constantes  et
et
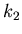 correspondant à ce sinogramme particulier sont données Tab.6.4.
correspondant à ce sinogramme particulier sont données Tab.6.4.
Table 6.4:
Constante
 et
et
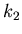 du sinogramme
du sinogramme
 .
.
|
|
Pour donner une idée de la variation de la constante 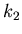 , nous avons
mémorisé les constantes
, nous avons
mémorisé les constantes 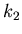 sur chacun des
sur chacun des  plans de projections
considérés. La moyenne de ces 10 constantes nous redonne la valeur optimale
obtenue graphiquement sur la figure Fig.6.4 (linéarité de la
moyenne). La variance de ces 10 valeurs nous permet de mettre un ordre de grandeur
sur la variation de la constante autour de sa moyenne. A titre d'illustration,
nous donnons les courbes analogues à celle obtenue Fig.6.7 pour
10 angles de vues
plans de projections
considérés. La moyenne de ces 10 constantes nous redonne la valeur optimale
obtenue graphiquement sur la figure Fig.6.4 (linéarité de la
moyenne). La variance de ces 10 valeurs nous permet de mettre un ordre de grandeur
sur la variation de la constante autour de sa moyenne. A titre d'illustration,
nous donnons les courbes analogues à celle obtenue Fig.6.7 pour
10 angles de vues  particuliers (Fig.6.8).
particuliers (Fig.6.8).
Figure 6.8:
 pour dix angles de vues
pour dix angles de vues
 .
.

|
Sur cette dernière (Fig.6.8) sont également tracées 10
lignes d'isocontour (valeur constante de  ). On constate que
pour suivre le fond de la vallée, i.e. pour suivre les valeurs optimales de
). On constate que
pour suivre le fond de la vallée, i.e. pour suivre les valeurs optimales de
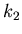 relative à chaque direction, nous nous déplaçons plus ou moins
sur une droite qui correspond à la valeur optimale de
relative à chaque direction, nous nous déplaçons plus ou moins
sur une droite qui correspond à la valeur optimale de 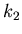 déjà mentionnée.
déjà mentionnée.
5.4.2.2 Test de Kolmogorov-Smirnov (KS).
Une autre façon de comparer les deux distributions ne nécessitant pas un calcul
d'histogramme passe par l'utilisation d'une statistique de Kolmogorov-Smirnov.
On considère dans ce cas le sinogramme de bruit sous une forme unidimensionnelle.
Nous avons  échantillons de nos distributions
échantillons de nos distributions
 et
et
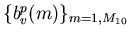 . Des estimateurs non biaisés des fonctions
de répartition de ces deux densités de probabilité
. Des estimateurs non biaisés des fonctions
de répartition de ces deux densités de probabilité
 et
et
 peuvent être construits. Ces fonctions de répartition
donnent la fraction de valeurs situées à gauche de
peuvent être construits. Ces fonctions de répartition
donnent la fraction de valeurs situées à gauche de  . Le test de KS se
base sur l'écart maximal observé entre ces fonctions de répartitions empiriques.
En effet, deux distributions différentes conduiront à des fonctions de repartition
différentes. Sous l'hypothèse
. Le test de KS se
base sur l'écart maximal observé entre ces fonctions de répartitions empiriques.
En effet, deux distributions différentes conduiront à des fonctions de repartition
différentes. Sous l'hypothèse 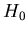 (les deux séries d'échantillons observées
proviennent de la même distribution), nous construisons la statistique suivante:
(les deux séries d'échantillons observées
proviennent de la même distribution), nous construisons la statistique suivante:
Nous pouvons pour chaque valeur de la constante 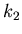 , estimer la valeur
de cette statistique. La valeur minimale de
, estimer la valeur
de cette statistique. La valeur minimale de
 nous conduit
à une constante
nous conduit
à une constante 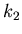 optimale. Pour le sinogramme
optimale. Pour le sinogramme  ,
nous obtenons les résultats illustrés Fig.6.9.
,
nous obtenons les résultats illustrés Fig.6.9.
Figure 6.9:
Courbe
 pour le sinogramme
pour le sinogramme

|
|
Nous constatons que l'utilisation de ce critère conduit à la même valeur de
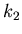 optimale. Comme précédemment, nous donnons les courbes
optimale. Comme précédemment, nous donnons les courbes
 pour 10 angles de vues particuliers (Fig.6.10)
pour 10 angles de vues particuliers (Fig.6.10)
Figure 6.10:
 pour 10 angles de vues
pour 10 angles de vues
 .
.
 |
.
Pour les valeurs optimales des constantes  et
et 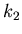 , les
histogrammes des deux sinogrammes de bruit sont donnés Fig.6.11.
, les
histogrammes des deux sinogrammes de bruit sont donnés Fig.6.11.
Figure 6.11:
Histogramme des sinogrammes de bruits. Les distributions sont normalisées par l'écart type du bruit sur les sinogrammes (Eq.6.9). On représente en bleu le sinogramme de bruit calculé et en vert le sinogramme de bruit réel.
 |
Il faut reconnaître une forte similitude entre les deux tracés. Le sinogramme
de bruit calculé présente donc bien le même type d'histogramme que le sinogramme
réel. Il faut noter un écart sur les faibles valeurs ( ) entre la
distribution calculée et la distribution réelle. Cette dernière présentant une
queue de distribution plus élevée. Si nous regardons, par segmentation de l'histogramme,
à quel endroit, spatialement, se situent les valeurs correspondant à cette queue
de distribution, nous constatons qu'il s'agit principalement de valeurs situées
à la périphérie du cerveau (i.e. à l'interface entre la tête et le fond).
) entre la
distribution calculée et la distribution réelle. Cette dernière présentant une
queue de distribution plus élevée. Si nous regardons, par segmentation de l'histogramme,
à quel endroit, spatialement, se situent les valeurs correspondant à cette queue
de distribution, nous constatons qu'il s'agit principalement de valeurs situées
à la périphérie du cerveau (i.e. à l'interface entre la tête et le fond).
D'autre part, on donne Fig.6.12 une illustration des sinogrammes
de bruit calculés et réels pour un même plan  . Même si les valeurs
de bruit se distribuent sensiblement de la même manière (histogrammes voisins),
la figure Fig.6.12
. Même si les valeurs
de bruit se distribuent sensiblement de la même manière (histogrammes voisins),
la figure Fig.6.12
Figure 6.12:
Deux plans  des sinogrammes de bruit.L'axe des abscisses correspond à une variation de
des sinogrammes de bruit.L'axe des abscisses correspond à une variation de  sur l'axe des ordonnées à une variation suivant
sur l'axe des ordonnées à une variation suivant 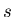 . La direction de projection
. La direction de projection
 est fixée.
est fixée.

|

|
[Sinogramme  ] ]
|
[Sinogramme  ] ]
|
met en évidence que les sinogrammes présentent en réalité un aspect sensiblement
différent. Pour le sinogramme de bruit calculé, nous n'avons pas un ``grain''
aussi fin que dans la distribution réelle. Cela est certainement un effet lié
au pas de discrétisation de notre volume qui reste, somme toute, relativement
grossier (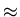 2mm).
2mm).
5.4.2.5 Confrontation des profils d'autocorrélation.
Nous avons montré précédemment que la corrélation suivant les angles de vues
 dépendait de la géométrie d'acquisition ainsi que du volume émetteur.
Il en va évidemment de même pour les angles d'inclinaison
dépendait de la géométrie d'acquisition ainsi que du volume émetteur.
Il en va évidemment de même pour les angles d'inclinaison  . En revanche,
nous avions supposé que les fonctions caractéristiques
. En revanche,
nous avions supposé que les fonctions caractéristiques
 correspondaient à des portions disjointes de l'espace lorsqu'on se déplacait
en
correspondaient à des portions disjointes de l'espace lorsqu'on se déplacait
en  où en
où en 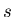 . Au moment de l'acquisition, nous avons un entrelaçage
des vues, et une valeur d'écartement nous permet de regrouper différentes lignes
de coïncidences au sein d'une même valeur de
. Au moment de l'acquisition, nous avons un entrelaçage
des vues, et une valeur d'écartement nous permet de regrouper différentes lignes
de coïncidences au sein d'une même valeur de 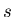 . L'ensemble de ces
techniques liées à l'acquisition vont induire une corrélation suivant les variables
. L'ensemble de ces
techniques liées à l'acquisition vont induire une corrélation suivant les variables
 et
et 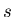 . Ces techniques (entrelaçage, brassage, écartement) ont
été prises en compte dans le calcul de notre sinogramme. Nous voulons donc voir
si ces éléments suffisent à expliquer la corrélation suivant ces deux directions
sur le sinogramme observé. Nous allons calculer les images d'autocorrélation
2D de chacun des 10 plans
. Ces techniques (entrelaçage, brassage, écartement) ont
été prises en compte dans le calcul de notre sinogramme. Nous voulons donc voir
si ces éléments suffisent à expliquer la corrélation suivant ces deux directions
sur le sinogramme observé. Nous allons calculer les images d'autocorrélation
2D de chacun des 10 plans  . Nous moyennons ensuite tous ces images
2D d'autocorrélation pour obtenir une image d'autocorrélation moyenne. D'autre
part, le fait de moyenner les différentes images de corrélation obtenues pour
chaque plan considéré nous fait perdre la variabilité de ces images en fonction
de l'angle de vue. Mais, il s'agit ici de déterminer si globalement suivant
les directions portées par
. Nous moyennons ensuite tous ces images
2D d'autocorrélation pour obtenir une image d'autocorrélation moyenne. D'autre
part, le fait de moyenner les différentes images de corrélation obtenues pour
chaque plan considéré nous fait perdre la variabilité de ces images en fonction
de l'angle de vue. Mais, il s'agit ici de déterminer si globalement suivant
les directions portées par  et
et  , les corrélations
entre sinogramme calculé et sinogramme réel sont les mêmes. Le moyennage a donc
un sens puisque dans les deux cas, le fantôme utilisé est le même et la géométrie
d'acquisition est la même. Sur la figure Fig.6.13
, les corrélations
entre sinogramme calculé et sinogramme réel sont les mêmes. Le moyennage a donc
un sens puisque dans les deux cas, le fantôme utilisé est le même et la géométrie
d'acquisition est la même. Sur la figure Fig.6.13
Figure:
Profils d'autocorrélation sur sinogramme de bruit calculé ou réel. On représente les profils suivant la direction  (à droite) et suivant la direction
(à droite) et suivant la direction  (à gauche) sur la même figure. Les profils vert (suivant
(à gauche) sur la même figure. Les profils vert (suivant  ) et rouge (suivant
) et rouge (suivant  ) correspondent au profils d'autocorrélation calculés pour le sinogramme de bruit réel (
) correspondent au profils d'autocorrélation calculés pour le sinogramme de bruit réel ( ), les profils bleu (suivant
), les profils bleu (suivant  ) et violet (suivant
) et violet (suivant  ) correspondent aux profils d'autocorrélation calculés pour le sinogramme de bruit calculé (
) correspondent aux profils d'autocorrélation calculés pour le sinogramme de bruit calculé ( )
)
 |
, nous représentons les profils moyens d'autocorrélation suivant les directions
associées à  et
et  . Ces profils d'autocorrélation
sont estimés dans l'espace de Fourier par utilisation des FFT. On considère
donc que le bruit est stationnaire sur chaque plan
. Ces profils d'autocorrélation
sont estimés dans l'espace de Fourier par utilisation des FFT. On considère
donc que le bruit est stationnaire sur chaque plan  . En effet, la
FFT ne nous donne accès qu'à une valeur globale de la corrélation. Les profils
d'autocorrélation sont donc uniquement fonction de
. En effet, la
FFT ne nous donne accès qu'à une valeur globale de la corrélation. Les profils
d'autocorrélation sont donc uniquement fonction de
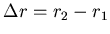 et
et
 et non plus de
et non plus de
 .5.5 Pour le sinogramme calculé, nous avons une corrélation beaucoup plus faible.
Il sera donc nécessaire d'introduire un filtrage ! Théoriquement, c'est le processus
d'émission des
.5.5 Pour le sinogramme calculé, nous avons une corrélation beaucoup plus faible.
Il sera donc nécessaire d'introduire un filtrage ! Théoriquement, c'est le processus
d'émission des
 qui est de nature poissonnienne et donc aléatoire.
Or, entre l'émission et la création de paires de photons
qui est de nature poissonnienne et donc aléatoire.
Or, entre l'émission et la création de paires de photons  , il
existe un parcours de l'anti-électron. Comme le sinogramme compte les paires
de photons, ce parcours va introduire un flou sur la localisation du bruit.
L'introduction d'un filtrage nous permet (en partie) de prendre en compte ce
flou.
, il
existe un parcours de l'anti-électron. Comme le sinogramme compte les paires
de photons, ce parcours va introduire un flou sur la localisation du bruit.
L'introduction d'un filtrage nous permet (en partie) de prendre en compte ce
flou.





Next: 5.5 Filtrage.
Up: 5. Bruit dans le
Previous: 5.3 Estimation des constantes.
Contents
Index
Lecomte Jean François
2002-09-07
![]() et
et ![]() .
.
![]() qui présente deux classes pour chacune des 2 substances
(
qui présente deux classes pour chacune des 2 substances
(![]() et
et ![]() ) présentant respectivement
) présentant respectivement ![]() et
et ![]() voxels. Les valeurs de chacune de ces deux substances sont dans le ratio
voxels. Les valeurs de chacune de ces deux substances sont dans le ratio
![]() ,
où
,
où ![]() représente la valeur moyenne sur la classe considérée. Seul le
ratio nous importe puisque c'est par la détermination de la constante
représente la valeur moyenne sur la classe considérée. Seul le
ratio nous importe puisque c'est par la détermination de la constante ![]() (Par.6.3.1)
que nous normalisons les projections calculées et donc notre volume par rapport
aux projections vraies. Cependant la valeur de la constante
(Par.6.3.1)
que nous normalisons les projections calculées et donc notre volume par rapport
aux projections vraies. Cependant la valeur de la constante ![]() est
liée aux valeurs affectées à chacune des deux classes. Si je choisis un fantôme
d'activité double pour la projection, la constante
est
liée aux valeurs affectées à chacune des deux classes. Si je choisis un fantôme
d'activité double pour la projection, la constante ![]() sera divisée
par deux. C'est pourquoi par la suite les valeurs des constantes
sera divisée
par deux. C'est pourquoi par la suite les valeurs des constantes ![]() seront données pour des valeurs du fantômes choisies en accord avec Tab.6.2.
seront données pour des valeurs du fantômes choisies en accord avec Tab.6.2.
![]() et
et ![]() . Nous allons donc définir une notion de région
. Nous allons donc définir une notion de région ![]() [16].
Un voxel
[16].
Un voxel ![]() 5.3 de l'image est considéré comme appartenant à la région
5.3 de l'image est considéré comme appartenant à la région ![]() si sa valeur
si sa valeur
![]() et si un certain
nombre de voxels de son voisinage sont dans le même intervalle de valeurs.
et si un certain
nombre de voxels de son voisinage sont dans le même intervalle de valeurs.
![]() représente une certaine tolérance par rapport à la moyenne. De ce fait, il est
nécessaire en plus de la moyenne
représente une certaine tolérance par rapport à la moyenne. De ce fait, il est
nécessaire en plus de la moyenne ![]() sur la région de définir la variance
sur la région de définir la variance
![]() sur cette région. Les valeurs pour le fantôme recalé sont consignées
dans les tableau Tab.6.3.
sur cette région. Les valeurs pour le fantôme recalé sont consignées
dans les tableau Tab.6.3.
![]() et
et ![]() . La démarche pour les obtenir est illustrée Fig.6.6
. La démarche pour les obtenir est illustrée Fig.6.6
![]() et
et ![]() pour un des sinogrammes de Tab.6.1. Nous allons
le faire pour le sinogramme présentant 260 M de coups (
pour un des sinogrammes de Tab.6.1. Nous allons
le faire pour le sinogramme présentant 260 M de coups (![]() ). La
détermination de la constante
). La
détermination de la constante ![]() ne pose aucun problème, elle s'obtient
directement grâce à Eq.6.3. Il faut noter toutefois que cette valeur
de constante est totalement dépendante des valeurs présentes dans le fantôme.
Cette constante est relative au fantôme décrit dans Tab.6.3.
La détermination de la constante
ne pose aucun problème, elle s'obtient
directement grâce à Eq.6.3. Il faut noter toutefois que cette valeur
de constante est totalement dépendante des valeurs présentes dans le fantôme.
Cette constante est relative au fantôme décrit dans Tab.6.3.
La détermination de la constante ![]() pose plus de problèmes. Nous allons
donc la déterminer graphiquement. Pour différentes valeurs de cette constante,
on calcule 10 plans de projections du sinogramme de bruit
pose plus de problèmes. Nous allons
donc la déterminer graphiquement. Pour différentes valeurs de cette constante,
on calcule 10 plans de projections du sinogramme de bruit
![]() .
Ces plans
.
Ces plans
![]() correspondent à 10 directions de projections
contenues dans le plan transaxial (10 valeurs de
correspondent à 10 directions de projections
contenues dans le plan transaxial (10 valeurs de ![]() pour
pour ![]() ).
Nous obtenons
).
Nous obtenons
![]() valeurs du sinogramme de
bruit
valeurs du sinogramme de
bruit
![]() à comparer aux
à comparer aux ![]() valeurs de
valeurs de ![]() prises pour les mêmes plans. Pour la comparaison, nous allons d'abord normaliser
chacune de ces deux portions de sinogramme. D'après l'Eq.6.8,
nous avons sur le sinogramme de bruit un bruit gaussien de variance en 3D égale
à
prises pour les mêmes plans. Pour la comparaison, nous allons d'abord normaliser
chacune de ces deux portions de sinogramme. D'après l'Eq.6.8,
nous avons sur le sinogramme de bruit un bruit gaussien de variance en 3D égale
à ![]() , il est nécessaire de déterminer les histogrammes. Ces deux
histogrammes comportent chacun
, il est nécessaire de déterminer les histogrammes. Ces deux
histogrammes comportent chacun ![]() classes. Le nombre de classes est
fonction du nombre d'échantillons choisis dans les sinogrammes de bruit et donc
de
classes. Le nombre de classes est
fonction du nombre d'échantillons choisis dans les sinogrammes de bruit et donc
de ![]() . La similarité entre ces deux histogrammes est alors mesurée
par le critère
. La similarité entre ces deux histogrammes est alors mesurée
par le critère ![]() défini par:
défini par:
![$\displaystyle \chi ^{2}=\sum ^{H_{m}}_{h_{i}=1}\frac{[g(h_{i})\vert _{b^{p}_{b}...
...\vert _{b^{p}_{v}}]^{2}}{g(h_{i})\vert _{b^{p}_{b}}+g(h_{i})\vert _{b^{p}_{v}}}$](img608.png)
![]() échantillons de nos distributions
échantillons de nos distributions
![]() et
et
![]() . Des estimateurs non biaisés des fonctions
de répartition de ces deux densités de probabilité
. Des estimateurs non biaisés des fonctions
de répartition de ces deux densités de probabilité
![]() et
et
![]() peuvent être construits. Ces fonctions de répartition
donnent la fraction de valeurs situées à gauche de
peuvent être construits. Ces fonctions de répartition
donnent la fraction de valeurs situées à gauche de ![]() . Le test de KS se
base sur l'écart maximal observé entre ces fonctions de répartitions empiriques.
En effet, deux distributions différentes conduiront à des fonctions de repartition
différentes. Sous l'hypothèse
. Le test de KS se
base sur l'écart maximal observé entre ces fonctions de répartitions empiriques.
En effet, deux distributions différentes conduiront à des fonctions de repartition
différentes. Sous l'hypothèse ![]() (les deux séries d'échantillons observées
proviennent de la même distribution), nous construisons la statistique suivante:
(les deux séries d'échantillons observées
proviennent de la même distribution), nous construisons la statistique suivante:
![]() et
et ![]() , les
histogrammes des deux sinogrammes de bruit sont donnés Fig.6.11.
, les
histogrammes des deux sinogrammes de bruit sont donnés Fig.6.11.

![]() . Même si les valeurs
de bruit se distribuent sensiblement de la même manière (histogrammes voisins),
la figure Fig.6.12
. Même si les valeurs
de bruit se distribuent sensiblement de la même manière (histogrammes voisins),
la figure Fig.6.12


![]() dépendait de la géométrie d'acquisition ainsi que du volume émetteur.
Il en va évidemment de même pour les angles d'inclinaison
dépendait de la géométrie d'acquisition ainsi que du volume émetteur.
Il en va évidemment de même pour les angles d'inclinaison ![]() . En revanche,
nous avions supposé que les fonctions caractéristiques
. En revanche,
nous avions supposé que les fonctions caractéristiques
![]() correspondaient à des portions disjointes de l'espace lorsqu'on se déplacait
en
correspondaient à des portions disjointes de l'espace lorsqu'on se déplacait
en ![]() où en
où en ![]() . Au moment de l'acquisition, nous avons un entrelaçage
des vues, et une valeur d'écartement nous permet de regrouper différentes lignes
de coïncidences au sein d'une même valeur de
. Au moment de l'acquisition, nous avons un entrelaçage
des vues, et une valeur d'écartement nous permet de regrouper différentes lignes
de coïncidences au sein d'une même valeur de ![]() . L'ensemble de ces
techniques liées à l'acquisition vont induire une corrélation suivant les variables
. L'ensemble de ces
techniques liées à l'acquisition vont induire une corrélation suivant les variables
![]() et
et ![]() . Ces techniques (entrelaçage, brassage, écartement) ont
été prises en compte dans le calcul de notre sinogramme. Nous voulons donc voir
si ces éléments suffisent à expliquer la corrélation suivant ces deux directions
sur le sinogramme observé. Nous allons calculer les images d'autocorrélation
2D de chacun des 10 plans
. Ces techniques (entrelaçage, brassage, écartement) ont
été prises en compte dans le calcul de notre sinogramme. Nous voulons donc voir
si ces éléments suffisent à expliquer la corrélation suivant ces deux directions
sur le sinogramme observé. Nous allons calculer les images d'autocorrélation
2D de chacun des 10 plans ![]() . Nous moyennons ensuite tous ces images
2D d'autocorrélation pour obtenir une image d'autocorrélation moyenne. D'autre
part, le fait de moyenner les différentes images de corrélation obtenues pour
chaque plan considéré nous fait perdre la variabilité de ces images en fonction
de l'angle de vue. Mais, il s'agit ici de déterminer si globalement suivant
les directions portées par
. Nous moyennons ensuite tous ces images
2D d'autocorrélation pour obtenir une image d'autocorrélation moyenne. D'autre
part, le fait de moyenner les différentes images de corrélation obtenues pour
chaque plan considéré nous fait perdre la variabilité de ces images en fonction
de l'angle de vue. Mais, il s'agit ici de déterminer si globalement suivant
les directions portées par ![]() et
et ![]() , les corrélations
entre sinogramme calculé et sinogramme réel sont les mêmes. Le moyennage a donc
un sens puisque dans les deux cas, le fantôme utilisé est le même et la géométrie
d'acquisition est la même. Sur la figure Fig.6.13
, les corrélations
entre sinogramme calculé et sinogramme réel sont les mêmes. Le moyennage a donc
un sens puisque dans les deux cas, le fantôme utilisé est le même et la géométrie
d'acquisition est la même. Sur la figure Fig.6.13
