




Next: 5.6 Estimation du modèle
Up: 5. Bruit dans le
Previous: 5.4 Confrontation du Modèle
Contents
Index
Subsections
Nous venons de constater (Fig.6.13) que la corrélation
sur le bruit ne dépend pas uniquement de la géométrie d'acquisition: elle varie
aussi avec la forme et l'intensité de l'objet lui-même (Par.6.3.2.4).
Cette dépendance vis à vis de l'objet imagé rend difficile la modélisation du
bruit sur les projections. Le noyau de filtrage à utiliser varie spatialement
et sa détermination doit se faire pour chaque objet imagé. C'est pourquoi, si
on conserve l'hypothèse que c'est principalement la projection qui induit une
corrélation variant spatialement et si on suppose également que la corrélation
pré-projection est invariante spatialement, alors nous pouvons envisager un
filtrage du volume servant à la projection par un noyau fixe. On peut donc filtrer
par simple multiplication dans l'espace de Fourier de l'objet. C'est le fait
de filtrer le volume avant projection qui va introduire la corrélation faisant
défaut au paragraphe Par.6.4.2.5.
D'autre part, on considère que la variance du bruit sur le volume dépend de
la distribution radioactive initiale. Nous bruitons le volume avant de le filtrer.
Ce filtrage, peut en quelque sorte matérialiser le parcours du  .
Les répercussions sur le protocole pour construire un sinogramme de bruit sont
illustrées Fig.6.14.
.
Les répercussions sur le protocole pour construire un sinogramme de bruit sont
illustrées Fig.6.14.
Figure:
Protocole pour créer numériquement un sinogramme de bruit.
|
|
Une deuxième question à laquelle il est nécessaire de répondre est la nature
du noyau de filtrage que nous allons utiliser. Le choix du noyau de filtrage
est un problème délicat, car le bruit en modifiant les valeurs du volume influe
sur la corrélation des projections. De plus, nous avons accès uniquement aux
projections bruitées et non au volume. A cette difficulté s'ajoutent des problèmes
liés à la discrétisation notamment dans le calcul des FFT.
On va définir un noyau pour chaque direction  ,
,  et
et 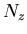 .
Les noyaux dans un plan transaxial seront les mêmes (
.
Les noyaux dans un plan transaxial seront les mêmes (
 ).
Le noyau global de filtrage tridimensionnel sera construit sur ces noyaux monodimensionnels:
).
Le noyau global de filtrage tridimensionnel sera construit sur ces noyaux monodimensionnels:
Par la suite  désigne l'un de ces noyaux monodimensionnels. Chaque noyau
désigne l'un de ces noyaux monodimensionnels. Chaque noyau
 sera décrit par 3 paramètres
sera décrit par 3 paramètres
 . Comme on
filtre avant projection, on fait l'hypothèse que les paramètres de ce noyau
ne dépendent ni de l'objet, ni du nombre de coups dans le volume. On va chercher
les paramètres à appliquer à tout volume émetteur, quel que soit son niveau
de bruit et sa forme, pour que les projections calculées à partir du volume
de bruit filtré présentent les mêmes caractéristiques en terme de corrélation
que les projections réelles. Autrement dit, on fait l'hypothèse que le variation
spatiale de la corrélation provient essentiellement de la projection.
. Comme on
filtre avant projection, on fait l'hypothèse que les paramètres de ce noyau
ne dépendent ni de l'objet, ni du nombre de coups dans le volume. On va chercher
les paramètres à appliquer à tout volume émetteur, quel que soit son niveau
de bruit et sa forme, pour que les projections calculées à partir du volume
de bruit filtré présentent les mêmes caractéristiques en terme de corrélation
que les projections réelles. Autrement dit, on fait l'hypothèse que le variation
spatiale de la corrélation provient essentiellement de la projection.
Tous les noyaux de filtrage utilisés sont des courbes en ``cloche'' permettant
de lisser le volume initial avant projection. Elles se caractérisent de la façon
suivante:
où  est un nombre fini.
est un nombre fini.
Dans notre étude, seuls deux noyaux ont été envisagés.
- Le noyau exponentiel
 défini par:
défini par:
- Le noyau de type sigmoïde
 défini par:
défini par:
Si ce deuxième type de noyau a été envisagé en plus des noyaux exponentiels,
c'est qu'il génère des corrélations qui ne décroissent pas aussi vite lorsque
 augmente. La forme générale de la corrélation ressemble au profil d'autocorrélation
obtenu avec ce type de noyau. Pour réduire encore le champ d'investigation,
nous avons considéré que
augmente. La forme générale de la corrélation ressemble au profil d'autocorrélation
obtenu avec ce type de noyau. Pour réduire encore le champ d'investigation,
nous avons considéré que  est à valeur entière. Seules les valeurs
est à valeur entière. Seules les valeurs
 pour le noyau sigmoïde et
pour le noyau sigmoïde et  pour le noyau
exponentiel ont été envisagées. D'autres cas ont été essayés mais ne seront
pas exposés, car ils ne conduisaient pas à des résultats probants. Nous verrons
pourquoi au Par.6.5.3.1.
pour le noyau
exponentiel ont été envisagées. D'autres cas ont été essayés mais ne seront
pas exposés, car ils ne conduisaient pas à des résultats probants. Nous verrons
pourquoi au Par.6.5.3.1.
On considère le sinogramme comme une série de plans de projection
 associés à la projection suivant
associés à la projection suivant  . Afin de déterminer les paramètres
et le type de noyau à utiliser, on va faire varier le triplet
. Afin de déterminer les paramètres
et le type de noyau à utiliser, on va faire varier le triplet
 .
Pour chaque triplet, on construit un sinogramme de bruit en accord avec le protocole
défini Fig.6.14. Les profils d'autocorrélation suivant deux
directions orthogonales (suivant
.
Pour chaque triplet, on construit un sinogramme de bruit en accord avec le protocole
défini Fig.6.14. Les profils d'autocorrélation suivant deux
directions orthogonales (suivant  et
et  ) dans chaque
plan sont calculés puis moyennés sur l'ensemble des directions
) dans chaque
plan sont calculés puis moyennés sur l'ensemble des directions  considérées.
considérées.  et
et  correspondent aux profils moyens déterminés
sur le sinogramme de bruit calculé et
correspondent aux profils moyens déterminés
sur le sinogramme de bruit calculé et  et
et  à ceux déterminés
sur le sinogramme de bruit calculé à partir de données réelles. Le critère
à ceux déterminés
sur le sinogramme de bruit calculé à partir de données réelles. Le critère  retenu pour choisir le meilleur filtre est calculé à partir de ces profils.
retenu pour choisir le meilleur filtre est calculé à partir de ces profils.
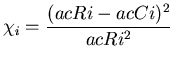 |
(5.10) |
où 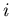 est soit
est soit 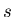 soit
soit  suivant que le profil est obtenu
suivant une direction associée à
suivant que le profil est obtenu
suivant une direction associée à  ou
ou  .
.
En pratique, pour déterminer l'ensemble des constantes
 et
et
 , nous fixons la vitesse de décroissance
, nous fixons la vitesse de décroissance  . Puis, pour
différentes valeurs du critère
. Puis, pour
différentes valeurs du critère  nous calculons par intégration la
constante de normalisation
nous calculons par intégration la
constante de normalisation 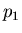 . Nous estimons alors la valeur du critère
défini par Eq.6.10. La détermination du minimum est graphique.
Le triplet optimal nous est fourni par la valeur de
. Nous estimons alors la valeur du critère
défini par Eq.6.10. La détermination du minimum est graphique.
Le triplet optimal nous est fourni par la valeur de  qui minimise
ce critère.
qui minimise
ce critère.
Pour chaque critère  , il est nécessaire de recalculer une valeur
optimale de
, il est nécessaire de recalculer une valeur
optimale de 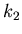 . Autrement dit, pour chaque détermination de
. Autrement dit, pour chaque détermination de
 ,
nous estimons la fonction
,
nous estimons la fonction
 , nous la minimisons et c'est
pour cette valeur optimale qu'est estimé le critère
, nous la minimisons et c'est
pour cette valeur optimale qu'est estimé le critère  .
.
Su les figures Fig.6.15.a,b,c
Figure 6.15:
Variation de  en fonction de
en fonction de  . On représente en vert la variation du critère suivant la direction
. On représente en vert la variation du critère suivant la direction  et en bleu celle suivant la direction
et en bleu celle suivant la direction  .
.

|

|

|
| [Noyau gaussien.]
|
[Noyau sigmoïde avec  .] .]
|
[Noyau sigmoïde avec  .] .]
|
sont représentées les variations du critère  pour les cas envisagés.
Globalement, nous observons sur chaque courbe un comportement analogue. En revanche,
on n'observe pas réellement de valeur optimale. On constate tout d'abord, une
zone plus ou moins constante du critère, puis, au delà d'une valeur seuil de
pour les cas envisagés.
Globalement, nous observons sur chaque courbe un comportement analogue. En revanche,
on n'observe pas réellement de valeur optimale. On constate tout d'abord, une
zone plus ou moins constante du critère, puis, au delà d'une valeur seuil de
 , le critère croit régulièrement. On a donc l'impression que dès
l'introduction d'un filtrage (
, le critère croit régulièrement. On a donc l'impression que dès
l'introduction d'un filtrage ( fois la taille du voxel!), le
filtre conduit à une corrélation proche de celle observée sur le sinogramme
réel. Ceci n'est pas vraiment le cas, car les profils d'autocorrélation montrent,
pour de petits écarts de
fois la taille du voxel!), le
filtre conduit à une corrélation proche de celle observée sur le sinogramme
réel. Ceci n'est pas vraiment le cas, car les profils d'autocorrélation montrent,
pour de petits écarts de  ou de
ou de  , une corrélation
calculée nettement supérieure à celle observée dans le cas réel . Le critère
n'est donc pas tout à fait optimal pour la sélection de la valeur
, une corrélation
calculée nettement supérieure à celle observée dans le cas réel . Le critère
n'est donc pas tout à fait optimal pour la sélection de la valeur  .
On considère toutefois que la valeur optimale de
.
On considère toutefois que la valeur optimale de  correspond au
moment où le critère décroche du plateau initial. Cette démarcation est très
nette dans le cas du noyau gaussien (Fig.6.17.a noyau exponentiel
avec
correspond au
moment où le critère décroche du plateau initial. Cette démarcation est très
nette dans le cas du noyau gaussien (Fig.6.17.a noyau exponentiel
avec  ). Elle l'est moins pour l'autre type de noyau envisagé (Fig.6.17.b
et c). Dans le tableau Tab.6.5.
). Elle l'est moins pour l'autre type de noyau envisagé (Fig.6.17.b
et c). Dans le tableau Tab.6.5.
sont consignées les valeurs optimales pour chacun des cas considérés. Sur les
figures Fig.6.16 et Fig.6.17 on donne, pour chaque
cas et pour un plan
 particulier, les histogrammes
particulier, les histogrammes
Figure:
Histogramme des sinogrammes de bruits pour différents types de noyaux construits avec les triplets optimaux
 (Tab.6.5). Les distributions sont normalisées par l'écart type du bruit sur les sinogrammes (Eq.6.9). On représente en bleu le sinogramme de bruit calculé et en vert le sinogramme de bruit réel.
(Tab.6.5). Les distributions sont normalisées par l'écart type du bruit sur les sinogrammes (Eq.6.9). On représente en bleu le sinogramme de bruit calculé et en vert le sinogramme de bruit réel.

|

|

|
| [Noyau gaussien.]
|
[Noyau sigmoïde avec  .] .]
|
[Noyau sigmoïde avec  .] .]
|
et les profils d'autocorrélation.
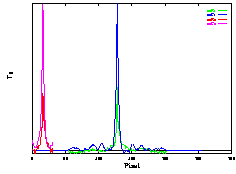
Figure:
Profils d'autocorrélation sur sinogramme de bruit calculé ou réel pour différents types de noyaux construits avec les triplets optimaux
 (Tab.6.5). On représente les profils suivant la direction
(Tab.6.5). On représente les profils suivant la direction  (à droite) et suivant la direction
(à droite) et suivant la direction  (à gauche) sur la même figure. Les profils vert (suivant
(à gauche) sur la même figure. Les profils vert (suivant  ) et rouge (suivant
) et rouge (suivant  ) correspondent aux profils d'autocorrélation calculés pour le sinogramme de bruit réel (
) correspondent aux profils d'autocorrélation calculés pour le sinogramme de bruit réel ( ), les profils bleu (suivant
), les profils bleu (suivant  ) et violet (suivant
) et violet (suivant  ) correspondent aux profils d'autocorrélation calculés pour le sinogramme de bruit calculé (
) correspondent aux profils d'autocorrélation calculés pour le sinogramme de bruit calculé ( )
)

|
|

|
| [Noyau gaussien.]
|
[Noyau sigmoïde avec  .] .]
|
[Noyau sigmoïde avec  .] .]
|
Nous venons de constater que les filtrages ``optimaux'' s'obtiennent pour
des valeurs très petites du paramètre 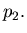 Par conséquent, les noyaux
se traduisent par des fonctions représentées par des pics très étroits (entre
Par conséquent, les noyaux
se traduisent par des fonctions représentées par des pics très étroits (entre
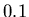 et
et 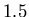 fois la taille du voxel). De ce fait, pour des petites
valeurs du paramètre
fois la taille du voxel). De ce fait, pour des petites
valeurs du paramètre  et une fois discrétisés, ces noyaux ont tous
des profils similaires où seul le voxel central est non nul (Fig.6.18).
et une fois discrétisés, ces noyaux ont tous
des profils similaires où seul le voxel central est non nul (Fig.6.18).
Figure 6.18:
Noyaux gaussien
 et sigmoïde
et sigmoïde
 pour
pour
 .
.
 |
Les corrélations induites sont, dans ce cas, semblables. Il faut faire croître
le paramètre  pour que les profils se différencient. D'autre part,
les profils des courbes, pour chacun des deux noyaux, ne varient pas de la même
manière en fonction du paramètre. Le noyau sigmoïde s'élargit plus rapidement
que le noyau gaussien lorsque
pour que les profils se différencient. D'autre part,
les profils des courbes, pour chacun des deux noyaux, ne varient pas de la même
manière en fonction du paramètre. Le noyau sigmoïde s'élargit plus rapidement
que le noyau gaussien lorsque  augmente. Sur les figures 6.19
et Fig.6.20, on représente les fonctions pour différentes valeurs
du paramètre
augmente. Sur les figures 6.19
et Fig.6.20, on représente les fonctions pour différentes valeurs
du paramètre  .
Pour améliorer les choses, il faudrait construire des filtres plus précis en
réduisant le pas d'échantillonnage spatial, c'est à dire diminuer la taille
des voxels des volumes utilisés pour la projection.
.
Pour améliorer les choses, il faudrait construire des filtres plus précis en
réduisant le pas d'échantillonnage spatial, c'est à dire diminuer la taille
des voxels des volumes utilisés pour la projection.
La distribution de bruit, une fois normalisée devrait suivre une loi normale
(de moyenne nulle et d'écart type égal à 1). Nous allons donc comparer l'histogramme
de la distribution de bruit  à celui obtenu pour une distribution
de bruit correspondant à une densité de probabilité normale.
à celui obtenu pour une distribution
de bruit correspondant à une densité de probabilité normale.
Dans un premier temps considérons la projection en l'absence de filtrage. Dans
ce cas, nous constatons (Fig.6.21.a)
Figure 6.21:
Comparaison des histogrammes avec la loi normale. On représente en vert l'histogramme normalisé (Eq.6.9) du sinogramme de bruit calculé  et en bleu celui qui correspond à une distribution suivant une loi normale.
et en bleu celui qui correspond à une distribution suivant une loi normale.

|

|
|
[Sans filtrage]
|
[Avec filrage gaussien]
|
que l'histogramme calculé s'étend plus qu'une loi normale (
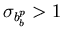 ).
Il faut chercher l'explication dans le fait que pour construire les plans de
détecteurs, nous intégrons l'information suivant plusieurs inclinaisons. Supposons
donc que
).
Il faut chercher l'explication dans le fait que pour construire les plans de
détecteurs, nous intégrons l'information suivant plusieurs inclinaisons. Supposons
donc que
 représente la loi statistique suivie par le sinogramme
de bruit pour une inclinaison particulière
représente la loi statistique suivie par le sinogramme
de bruit pour une inclinaison particulière  . Pour simplifier,
nous envisageons le cas où toutes ces lois sont de variance
. Pour simplifier,
nous envisageons le cas où toutes ces lois sont de variance
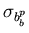 .
Du fait, de l'écartement, nous intégrons dans un plan de détecteurs l'information
provenant de
.
Du fait, de l'écartement, nous intégrons dans un plan de détecteurs l'information
provenant de 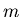 inclinaisons différentes (où
inclinaisons différentes (où 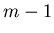 suivant la parité
du plan et du segment considéré cf Ch.4). La loi statistique
suivie par le sinogramme de bruit correspond donc à la somme des lois
suivant la parité
du plan et du segment considéré cf Ch.4). La loi statistique
suivie par le sinogramme de bruit correspond donc à la somme des lois
 pour les
pour les 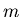 angles
angles  contribuant au sinogramme de bruit.
Donc, si maintenant nous cherchons la variance de la loi
contribuant au sinogramme de bruit.
Donc, si maintenant nous cherchons la variance de la loi
 effectivement suivie par le sinogramme de bruit, nous obtenons:
D'un autre côté, les variables
effectivement suivie par le sinogramme de bruit, nous obtenons:
D'un autre côté, les variables
 sont corrélées et vu les
angles
sont corrélées et vu les
angles  voisins considérés, les lois
voisins considérés, les lois
 ont
tendance à fluctuer dans la même direction. Le terme de covariance sera donc
positif. En l'absence de corrélation, nous aurions:
ont
tendance à fluctuer dans la même direction. Le terme de covariance sera donc
positif. En l'absence de corrélation, nous aurions:
 |
(5.11) |
Et si nous avions 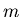 fois la même loi, nous aurions:
fois la même loi, nous aurions:
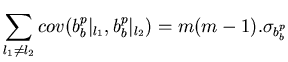 |
(5.12) |
Les équations Eq.6.11 et Eq.6.12 nous
donnent respectivement un minorant et un majorant pour ce terme de covariance.
Ainsi, nous pouvons trouver un intervalle pour la variance dans un plan de détecteur
qui vaut:
La variance que nous observons réellement dans un plan est supérieure à celle
que nous avons pour une seule inclinaison. Autrement dit, dans la normalisation
effectuée (Eq.6.9), nous ne normalisons pas suffisamment
(Fig.6.21.a). La normalisation devrait être:
où
 . Nous n'avons pas besoin de calculer cette constante
pour construire un sinogramme, car elle s'introduit de façon naturelle dans
notre projection. Ce défaut sur la normalisation ne modifie pas la nature de
la gaussienne obtenue. Il y a juste que nous ne pouvons pas comparer l'histogramme
des valeurs avec la loi normale de façon directe.
. Nous n'avons pas besoin de calculer cette constante
pour construire un sinogramme, car elle s'introduit de façon naturelle dans
notre projection. Ce défaut sur la normalisation ne modifie pas la nature de
la gaussienne obtenue. Il y a juste que nous ne pouvons pas comparer l'histogramme
des valeurs avec la loi normale de façon directe.
Dans tous les développements précédents, nous avons accepté l'hypothèse de non-corrélation
sur notre bruit (Eq.6.8). Or, le filtrage effectué avant projection
introduit une corrélation et infirme cette hypothèse. Toutefois, ce filtrage
étant linéaire, nous n'altérons pas la nature du bruit sur le sinogramme (l'histogramme
des valeurs reste gaussien). Cependant, le filtrage réduit la variance du sinogramme
de bruit de sorte que la normalisation nous conduit à une constante  .
(Fig.6.21.b). Pour estimer la variable
.
(Fig.6.21.b). Pour estimer la variable  , nous
cherchons a posteriori la largeur à mi-hauteur de l'histogramme de bruit
que nous rapportons à la hauteur à mi-hauteur de l'histogramme relatif à la
loi normale.
, nous
cherchons a posteriori la largeur à mi-hauteur de l'histogramme de bruit
que nous rapportons à la hauteur à mi-hauteur de l'histogramme relatif à la
loi normale.
Nous pouvons donc maintenant résumer le noyau de filtrage que nous utiliserons.
Au vu des résultats précédents, nous n'envisageons pas le même type de noyau
suivant la direction ( ou
ou  ). Dans la direction portée
par
). Dans la direction portée
par  nous utilisons un noyau gaussien alors que suivant la direction
nous utilisons un noyau gaussien alors que suivant la direction
 nous envisageons un noyau sigmoïde. Le tableau Tab.6.6
résume, toujours pour le sinogramme
nous envisageons un noyau sigmoïde. Le tableau Tab.6.6
résume, toujours pour le sinogramme  , l'intégralité des constantes.
, l'intégralité des constantes.





Next: 5.6 Estimation du modèle
Up: 5. Bruit dans le
Previous: 5.4 Confrontation du Modèle
Contents
Index
Lecomte Jean François
2002-09-07
![]() .
Les répercussions sur le protocole pour construire un sinogramme de bruit sont
illustrées Fig.6.14.
.
Les répercussions sur le protocole pour construire un sinogramme de bruit sont
illustrées Fig.6.14.
![]() ,
, ![]() et
et ![]() .
Les noyaux dans un plan transaxial seront les mêmes (
.
Les noyaux dans un plan transaxial seront les mêmes (
![]() ).
Le noyau global de filtrage tridimensionnel sera construit sur ces noyaux monodimensionnels:
).
Le noyau global de filtrage tridimensionnel sera construit sur ces noyaux monodimensionnels:

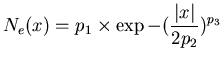
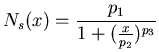
![]() associés à la projection suivant
associés à la projection suivant ![]() . Afin de déterminer les paramètres
et le type de noyau à utiliser, on va faire varier le triplet
. Afin de déterminer les paramètres
et le type de noyau à utiliser, on va faire varier le triplet
![]() .
Pour chaque triplet, on construit un sinogramme de bruit en accord avec le protocole
défini Fig.6.14. Les profils d'autocorrélation suivant deux
directions orthogonales (suivant
.
Pour chaque triplet, on construit un sinogramme de bruit en accord avec le protocole
défini Fig.6.14. Les profils d'autocorrélation suivant deux
directions orthogonales (suivant ![]() et
et ![]() ) dans chaque
plan sont calculés puis moyennés sur l'ensemble des directions
) dans chaque
plan sont calculés puis moyennés sur l'ensemble des directions ![]() considérées.
considérées. ![]() et
et ![]() correspondent aux profils moyens déterminés
sur le sinogramme de bruit calculé et
correspondent aux profils moyens déterminés
sur le sinogramme de bruit calculé et ![]() et
et ![]() à ceux déterminés
sur le sinogramme de bruit calculé à partir de données réelles. Le critère
à ceux déterminés
sur le sinogramme de bruit calculé à partir de données réelles. Le critère ![]() retenu pour choisir le meilleur filtre est calculé à partir de ces profils.
retenu pour choisir le meilleur filtre est calculé à partir de ces profils.
![]() et
et
![]() , nous fixons la vitesse de décroissance
, nous fixons la vitesse de décroissance ![]() . Puis, pour
différentes valeurs du critère
. Puis, pour
différentes valeurs du critère ![]() nous calculons par intégration la
constante de normalisation
nous calculons par intégration la
constante de normalisation ![]() . Nous estimons alors la valeur du critère
défini par Eq.6.10. La détermination du minimum est graphique.
Le triplet optimal nous est fourni par la valeur de
. Nous estimons alors la valeur du critère
défini par Eq.6.10. La détermination du minimum est graphique.
Le triplet optimal nous est fourni par la valeur de ![]() qui minimise
ce critère.
qui minimise
ce critère.
![]() , il est nécessaire de recalculer une valeur
optimale de
, il est nécessaire de recalculer une valeur
optimale de ![]() . Autrement dit, pour chaque détermination de
. Autrement dit, pour chaque détermination de
![]() ,
nous estimons la fonction
,
nous estimons la fonction
![]() , nous la minimisons et c'est
pour cette valeur optimale qu'est estimé le critère
, nous la minimisons et c'est
pour cette valeur optimale qu'est estimé le critère ![]() .
.









![]() Par conséquent, les noyaux
se traduisent par des fonctions représentées par des pics très étroits (entre
Par conséquent, les noyaux
se traduisent par des fonctions représentées par des pics très étroits (entre
![]() et
et ![]() fois la taille du voxel). De ce fait, pour des petites
valeurs du paramètre
fois la taille du voxel). De ce fait, pour des petites
valeurs du paramètre ![]() et une fois discrétisés, ces noyaux ont tous
des profils similaires où seul le voxel central est non nul (Fig.6.18).
et une fois discrétisés, ces noyaux ont tous
des profils similaires où seul le voxel central est non nul (Fig.6.18).
![]() à celui obtenu pour une distribution
de bruit correspondant à une densité de probabilité normale.
à celui obtenu pour une distribution
de bruit correspondant à une densité de probabilité normale.


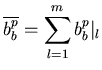

![]() .
(Fig.6.21.b). Pour estimer la variable
.
(Fig.6.21.b). Pour estimer la variable ![]() , nous
cherchons a posteriori la largeur à mi-hauteur de l'histogramme de bruit
que nous rapportons à la hauteur à mi-hauteur de l'histogramme relatif à la
loi normale.
, nous
cherchons a posteriori la largeur à mi-hauteur de l'histogramme de bruit
que nous rapportons à la hauteur à mi-hauteur de l'histogramme relatif à la
loi normale.
![]() ou
ou ![]() ). Dans la direction portée
par
). Dans la direction portée
par ![]() nous utilisons un noyau gaussien alors que suivant la direction
nous utilisons un noyau gaussien alors que suivant la direction
![]() nous envisageons un noyau sigmoïde. Le tableau Tab.6.6
résume, toujours pour le sinogramme
nous envisageons un noyau sigmoïde. Le tableau Tab.6.6
résume, toujours pour le sinogramme ![]() , l'intégralité des constantes.
, l'intégralité des constantes.