9.3 Procédures accélérées.

Même si l'ensemble des procédures ont été écrites dans un souci de rapidité, nous allons insister plus particulièrement sur 2 procédures: la rétroprojection et le calcul du produit matriciel $\mathbf{H}^{t}\mathbf{Hf}$ impliqué dans la reconstruction algébrique. Ces deux procédures en effet, montrent comment on peut tirer parti de la puissance de calcul du CRAY à l'aide des simples notions que nous avons introduites précédemment.

9.3.1 La rétroprojection.

La rétroprojection est un mécanisme essentiel dans la reconstruction d'images. Si on raisonne en 2D et si l'image est décrite sur une base de pixels, sa taille est de dimensions $n^{2}=N_{x}\times N_{y}$. Un algorithme conventionnel comme l'algorithme de Shepp et Logan requiert $O(n^{2})$ multiplications et $O(n^{2})$ additions. En passant en 3D, la complexité passe à $O(n^{3})$. Ce surcoût de calcul reste encore à l'heure actuelle un handicap.^9.4 C'est pourquoi, il s'avère impératif de réduire le temps de calcul nécessaire à la rétroprojection. Les tentatives faites en ce sens peuvent être regroupées en trois catégories:

• Amélioration au niveau algorithmique.
• Conception de matériel spécifiquement dédié.
• Recours au parallélisme.

Dans la première catégorie, citons notamment l'algorithme STRETCH [78] qui effectue une interpolation linéaire approximative en se servant de tables précompilées, mais aussi l'algorithme incrémental de Cho[18], mal adapté à notre architecture [20], et destiné à limiter sensiblement le nombre de multiplications. Une implémentation efficace en a été proposée par Egger[33].

Concernant la deuxième catégorie, des solutions spécifiques ont été mises en place. Par exemple, un circuit spécialement conçu pour l'algorithme STRETCH a été utilisé par [96]. Plus récemment, un circuit permettant d'effectuer une interpolation bilinéaire nécessaire à la reconstruction 3D a été proposé [47]. Les temps de rétroprojection sont alors inférieurs à la minute.

Finalement le recours au parallélisme est une idée séduisante. D'une part par les fermes de PCs qui voient le jour actuellement. Et plus particulièrement au centre CYCERON puisqu'elle peut être facilement adaptée de manière performante à la machine dont nous disposons.

9.3.1.1 Présentation de l'algorithme en 2D.

Rappelons que la projection bidimensionnelle analytique nous avait amené à écrire:

$$p(r,\theta )=\int \int _{x,y}f(x,y)\Phi _{r,\theta }(x,y)dxdy$$

où $\Phi _{r,\theta }$ est une fonction caractéristique qui spécifie un ``faisceau'' pour l'intégration des contributions de l'image.

Inversement, la rétroprojection consiste à affecter en chaque point $(x_{E},y_{E})$ d'une image $e_{\theta }(x,y)$ la valeur de toutes les projections $p(r,\theta )$ pour tous les couples $(r,\theta )$ tels que $\Phi _{r,\theta }(x_{E},y_{E})=1.$ Ceci correspond à une étape de localisation qui consiste à chercher quels sont les couples $(r,\theta )$ ou ``faisceaux'' qui voient ce pixel précis.

L'interpolation représente la deuxième étape majeure de la rétroprojection. Il s'agit de la pondération des contributions des différents faisceaux à un pixel particulier.

La localisation consiste à récupérer, pour un angle de vue particulier, l'indice $r_{i}$ de la projection la plus proche et donc du faisceau le plus proche contenant le point $E$ considéré (Fig.10.6).

Figure: Notations pour l'algorithme de rétroprojection.

Ensuite comme l'abscisse $r$ de la projection de $E$ suivant cette direction $\theta$ ne conduit pas au centre du détecteur référencé par $r_{i}$, on définit la distance $d_{i}=r-r_{i}$ et on procède ensuite à une interpolation (classiquement une interpolation linéaire). La valeur affectée en $e_{\theta }(x_{E},y_{E})$ est alors:

$$e_{\theta }(x_{E},y_{E})=\frac{r_{i+1}-r_{i}-d_{i}}{r_{i+1}-r_{i}}p(r_{i},\theta )+\frac{d_{i}}{r_{i+1}-r_{i}}p(r_{i+1},\theta )$$ (9.1)

La rétroprojection complète s'obtient ensuite par une sommation sur tous les angles de vue possibles:

$$e(x_{E},y_{E})=\sum _{\theta }e_{\theta }(x_{E},y_{E})$$

9.3.1.2 Algorithme de Shepp et Logan.

Cet algorithme s'appuie sur le fait que notre image est discrétisée dans une base de pixels. Dans cette base, les déplacements pour passer du centre d'un pixel au centre d'un autre pixel suivant la direction $x$ (ou suivant la direction $y$) sont quantifiés par la la taille $\Delta x$ (ou $\Delta y$) du pixel suivant cette direction. Tout déplacement correspond à un multiple de $\Delta x$ (ou $\Delta y$). De ce fait, pour un angle de vue $\theta$ donné, ce déplacement suivant $x$ (resp. $y$) une fois projeté conduit à un incrément $dr_{x}$ suivant la direction $r$ tel que: $dr_{x}=-\sin \theta \times \Delta x$ (resp. $dr_{y}=\cos \theta \times \Delta x$). Il en découle alors l'algorithme Alg.7

9.3.1.3 Algorithme de Shepp et Logan en 3D.

Même si les auteurs ne précisent pas l'extension au cas 3D, il se déduit assez facilement de l'algorithme bidimensionnel. Dans l'étape de localisation, il sera alors nécessaire de repérer les valeurs $r_{i}$ et $s_{j}$ les plus proches du point $(r,s,\theta ,\phi )$ correspondant à la projection d'un voxel $(x,y,z)$ ainsi que les distances $d_{i}=r-r_{i}$ et $d_{j}=s-s_{j}$. L'interpolation deviendra une interpolation bilinéaire:

$$e_{\theta ,\phi }(x,y,z) = \frac{1}{(r_{i+1}-r_{i}).(s_{j+1}-s_{j})}$$

$$\times [(r_{i+1}-r_{i}-d_{i}).(s_{j+1}-s_{j}-d_{j}).p(r_{i},s_{j},\theta ,\phi )+d_{i}.d_{j}.p(r_{i+1},s_{j+1},\theta ,\phi )$$

$$+d_{i}.(s_{j+1}-s_{j}-d_{j}).p(r_{i+1},s_{j},\theta ,\phi )+(r_{i+1}-r_{i}-d_{i}).d_{j}.p(r_{i},s_{j+1},\theta ,\phi )]$$

La rétroprojection consistera ensuite à effectuer une sommation pour tous les couples $(\theta ,\phi )$ qui fixent une direction de projection.

$$e(x,y,z)=\sum _{\theta }\sum _{\phi }e_{\theta ,\phi }(x,y,x)$$

On peut exprimer cette interpolation différemment:

$$e_{\theta ,\phi }(x,y,z) = \frac{1}{(r_{i+1}-r_{i}).(s_{j+1}-s_{j})}$$

$$\times [p(r_{i},s_{j,}\theta ,\phi )+d_{i}.K_{1}+d_{j}.K_{2}+d_{i}.d_{j}K_{3}]$$

où:

$$K_{1} = (s_{j+1}-s_{j}).[p(r_{i+1},s_{j},\theta ,\phi )-p(r_{i},s_{j},\theta ,\phi )]$$

$$K_{2} = (r_{i+1}-r_{i}).[p(r_{i},s_{j+1},\theta ,\phi )-p(r_{i},s_{j},\theta ,\phi )]$$

$$K_{3} = p(r_{i+1},s_{j+1},\theta ,\phi )-p(r_{i+1},s_{j},\theta ,\phi )+p(r_{i},s_{j},\theta ,\phi )-p(r_{i},s_{j+1},\theta ,\phi )$$

L'interpolation écrite sous cette forme nous permet de diminuer le nombre d'opérations élémentaires nécessaires à son calcul. En effet, les constantes $K_{1}$, $K_{2}$ et $K_{3}$ peuvent être calculées et mémorisées en dehors de la boucle effectuant la sommation sur toutes les directions $(\theta ,\phi )$.

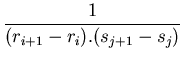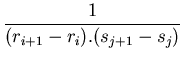Pour implémenter l'algorithme de Shepp et Logan en 3D, il faut également définir, suivant les directions $r$ et $s$, les incréments associés à la projection des déplacements unitaires sur le volume suivant les directions $x$,$y$ et $z$.

$$dr_{x} = -\sin \theta \times \Delta x$$

$$dr_{y} = \cos \theta \times \Delta y$$

$$dr_{z} =$$ 0

$$ds_{x} = -\cos \theta \sin \phi \times \Delta x$$

$$ds_{y} = -\sin \theta \sin \phi \times \Delta y$$

$$ds_{z} = \cos \phi \times \Delta z$$

Le calcul des cosinus et sinus étant une opération coûteuse en temps de calcul, on calcule au préalable des tables de cosinus et sinus que l'on mémorise. On remplace ainsi le calcul par un accès mémoire.

On peut donc maintenant donner une version de l'algorithme de rétroprojection 3D (Alg.8).

L'interpolation intervient au coeur de cinq boucles imbriquées. On comprend alors l'importance d'avoir diminué le nombre d'opérations requises pour son calcul. D'autre part, la condition concernant la validité du capteur provient du fait que certains voxels ne sont pas vus par tous les détecteurs (géométrie cylindrique d'acquisition et caractère fini du sinogramme).

On constate que la valeur de $r_{x,y,z}$ correspondant à la coordonnée suivant $\vec{r}$ dans le plan de projection $\Pi _{\theta ,\phi }$ est uniquement dépendante des coordonnées $(x,y)$ du voxel projeté ($dr_{z}=0$). L'idée est donc d'inverser l'ordre des boucles $z,y,x$ par $x,y,z$, de sorte qu'avant de rentrer dans la boucle sur les $z$, nous puissions d'ores et déjà calculer $r_{x,y,z}=r_{x,y}$. Si cette valeur $r_{x,y,z}$ conduit à un indice n'appartenant pas au sinogramme discret, nous pouvons ainsi éviter une boucle sur les $z$. Ceci est important puisque c'est la boucle la plus externe qui est parallélisée. Après inversion de l'ordre, la boucle sur les $x$ correspond à la boucle la plus externe.

Les accès mémoires sont importants et l'inversion de l'ordre de parcours du volume conduit à un adressage qui n'est plus optimal avec la façon dont l'ordinateur lit en mémoire. C'est pourquoi dans la rétroprojection, nous construisons un volume $e_{envers}(z,y,x)$ que nous permutons à la fin de la procédure pour obtenir $e(x,y,z)$. L'algorithme de rétroprojection devient Alg.9.

Nous pouvons également, dans certains cas, faire intervenir des symétries permettant de minimiser la nombre d'itérations des différentes boucles [20]. D'une manière générale, dans l'ensemble des procédures, nous essayons de limiter le nombre de divisions à l'intérieur des boucles, car cette opération coûteuse requiert trois multiplications et une réciproque.

9.3.2 Reconstruction algébrique par Gradient Conjugué.

Rappelons que la reconstruction algébrique implique le système linéaire:

$$\mathbf{p}=\mathbf{Hf}+\mathbf{b}$$

Dans cette expression, $H_{mn}$ représente la fraction de photons émise du voxel $f_{n}$ et détectée au niveau du détecteur $p_{m}$. Ce système nous avait conduit à résoudre le système d'équations linéaires suivant:

$$\mathbf{Af} = \mathbf{c}$$

$$(\mathbf{H}^{t}\Gamma ^{-1}_{b}\mathbf{Hf}-\Delta _{pond}\mathbf{f}) = \mathbf{H}^{t}\mathbf{p}$$

On suppose par la suite que la matrice de Variance-Covariance du bruit, dans la résolution du système, peut se mettre sous la forme d'une matrice diagonale telle que: $\Gamma ^{-1}_{b}=\sigma \times \mathbf{Id}$ où $\sigma$ représente la variance du bruit et $\mathbf{Id}$ la matrice identité. Le système est donc:

$$(\mathbf{H}^{t}\mathbf{Hf}-\Delta _{pond}\mathbf{f})=\mathbf{H}^{t}\mathbf{p}$$ (9.2)

Notre méthode de reconstruction algébrique, par le biais de l'équation matricielle (10.2), nous conduit à de nombreux produits matriciels. En effet, à chaque itération de l'algorithme 6, il est nécessaire de recalculer le produit $\mathbf{H}^{t}\mathbf{Hf}$. En regardant ce que représente une multiplication par $\mathbf{H}$ d'une part, et une multiplication par $\mathbf{H}^{t}$ d'autre part et en acceptant l'hypothèse simplificatrice sur le bruit, cela nous permettra de construire directement la matrice $\mathbf{H}^{t}\mathbf{H}$ (opération coûteuse en temps de calcul) et surtout d'en réduire considérablement la taille mémoire sans altérer les performances de calcul du produit $\mathbf{H}^{t}\mathbf{Hf}$ (opération hautement vectorisable et parallélisable).

9.3.2.1 Multiplication par $\mathbf{H}$.

Cette opération revient à faire la projection d'une image. En effet, partant d'un vecteur $\mathbf{f}$ de dimensions $[N,1]$ (égales au nombre de voxels dans un volume émetteur), on obtient par l'utilisation d'une matrice de dimensions $[M,N]$ un vecteur de dimensions $[M,1]$ (égales au nombre de détecteurs dans le sinogramme).

$$p_{m}=\sum _{n}H_{mn}f_{n}$$ (9.3)

représente la somme de toutes les contributions des différentes portions de l'image $f_{n}$, pondérée par leur probabilité $H_{mn}$ d'être détectée en $m$. On trouve ainsi les valeurs récoltées au niveau des capteurs $\mathbf{p}$ pour une distribution d'activité $\mathbf{f}$.

Pour une matrice $\mathbf{H}$ connue, la réponse impulsionnelle sur les détecteurs pour une source ponctuelle s'obtient en considérant un vecteur $\mathbf{f}$ (une image) non nul pour une seule de ses composantes (sorte de dirac discret) et par l'application de Eq.10.3. Inversement, dans la colonne $n$ de $\mathbf{H}$ est stockée la réponse impulsionnelle sur les $M$ détecteurs pour une source ponctuelle unitaire placée en $n$ (Fig.10.7).

Figure: Matrice $\mathbf{H}$ et réponse impulsionnelle (cas 2D). On affecte dans une colonne de $\mathbf{H}$ la réponse impulsionnelle d'une source ponctuelle unitaire placée en $n$ (les gaussiennes bleues représentent les réponses impulsionnelles suivant les différents angles de vues $\theta$).

9.3.2.2 Multiplication par $\mathbf{H}^{t}$.

Cette opération consiste à faire la rétroprojection (backprojection) d'une série de mesure $\mathbf{p}$ sur les détecteurs. En effet, partant d'un vecteur $\mathbf{p}$ de dimensions $[M,1]$ (égales au nombre de détecteurs dans le sinogramme), on obtient par l'utilisation d'une matrice de dimensions $[N,M]$ un vecteur de dimensions $[N,1]$ (égales au nombre de voxels dans un volume émetteur)

$$f_{n}=\sum _{m}H_{mn}p_{m}\Leftrightarrow \mathbf{f}=\mathbf{H}^{t}\mathbf{p}$$

Cela consiste à affecter à la composante $n$ d'un vecteur image $\mathbf{f}$, les contributions de chacun des détecteurs $p_{m}$, pondérées par la réponse impulsionnelle du dit voxel (Fig.10.8).

Figure: Matrice $\mathbf{H^t}$ et rétroprojection (cas 2D). La valeur affectée à la composante $f_n$ est la somme des contributions (aires hachurées sous la gaussienne noire) de chaque détecteur (les gaussiennes bleues représentent les réponses mesurées par les détecteurs) pondérées par la réponse impulsionnelle d'une source ponctuelle placée en $n$ (la gaussienne rouge représente la pondération)

9.3.2.3 Construction théorique de $\mathbf{H}^{t}\mathbf{H}$.

Notons que dans le cas tridimensionnel, la matrice $\mathbf{H}_{3D}$ est de dimension conséquente ( $[N_{r}\times N_{s}\times N_{\theta }\times N_{\phi },N_{x}\times N_{y}\times N_{z}]$). C'est pourquoi nous envisageons la reconstruction algébrique après rebinning. Le sinogramme sera donc de taille $N_{\phi }$ fois plus petite. Mais surtout le rebinning décompose le problème de reconstruction 3D en une série de reconstructions 2D par tranche. Autrement dit, on peut considérer une matrice $\mathbf{H}_{2Dz}$ par tranche transaxiale. Chaque matrice n'est plus alors que de dimension $[N_{r}\times N_{\theta },N_{x}\times N_{y}]$. Si du plus, nous considérons une invariance de la matrice $\mathbf{H}_{2Dz}$ suivant la direction $z$, nous avons alors une seule matrice (notée $\mathbf{H}$ par la suite) pour les $N_{z}$ plans à reconstruire. De ce fait, nous travaillons maintenant en 2D. La reconstruction consiste alors partant d'un sinogramme ``rebinné'' à estimer le volume en calculant $N_{z}$ images 2D. Ceci nous permet de paralléliser avec une forte granularité, car nous obtenons une indépendance entre les $N_{z}$ reconstructions. Nous pouvons donc maintenant poursuivre le raisonnement en 2D en envisageant la reconstruction d'un plan transaxial précis.

Par la suite, nous faisons les hypothèses supplémentaires:

• la réponse impulsionnelle $h$ de la caméra est indépendante de la position $(x,y)$ d'une source ponctuelle dans l'image.
• la réponse impulsionnelle est gaussienne d'écart type $\sigma$

Autrement dit, si $r_{1}$ représente la coordonnée de la projection suivant la direction définie par l'angle $\theta$ de la composante $n_{1}$ de l'image $\mathbf{f}$, alors la contribution de ce pixel au capteur situé en $r_{1}+r$ est :

$$h(r_{1}+r)=\frac{1}{\sigma \sqrt{2\pi }}e^{\frac{-[r_{1}-(r_{1}+r... ...2}}{2\sigma ^{2}}}=\frac{1}{\sigma \sqrt{2\pi }}e^{\frac{-r^{2}}{2\sigma ^{2}}}$$ (9.4)

9.3.2.4 Signification et calcul du produit $\mathbf{H}^{t}\mathbf{H}$.

Une fois l'invariance de la réponse impulsionnelle posée, on peut chercher les redondances présentes dans la matrice produit $\mathbf{H}^{t}\mathbf{H}$ et donc réduire calculs et espace mémoire en construisant directement cette matrice. On s'affranchit ainsi de la construction de la matrice $\mathbf{H}$ et du produit matriciel $\mathbf{H}^{t}\mathbf{H}$.

Considérons deux composantes $n_{1}$ et $n_{2}$ du vecteur image. Exprimer le produit $\mathbf{H}^{t}\mathbf{H}$, c'est chercher à exprimer la rétroprojection en $n_{2}$ de la projection d'une source ponctuelle placée en $n_{1}$. La valeur de $(H^{t}H)_{n_{1},n_{2}}$ est la somme des contributions de chaque détecteur pondérées par la réponse impulsionnelle d'une source ponctuelle placée en $n_{1}$(Fig.10.8 et Fig. 10.9 ).

Figure: Construction de $\mathbf{H}^{t}\mathbf{H}$

Fixons une direction de projection $\theta$ et notons par $d$ la distance qui sépare les droites de projection suivant $\theta$ relatives à $n_{1}$ et $n_{2}$. $r_{1}$ représente toujours l'abscisse de la projection suivant $\theta$ de $f_{n_{1}}$ (Fig. 10.9 ). $r_{1}$ comme $d$ sont dépendants de $\theta$ ( $r_{1}(\theta ),d(\theta )$). Nous avons donc :

$$(H^{t}H)_{n_{2},n_{1}}=\int _{0}^{\pi }\int _{\infty }^{\infty }h(r_{1}+r)h(r_{1}+r+d)drd\theta$$ (9.5)

avec $h(r_{1}+r)$ calculé en accord avec Eq.10.4. On sépare le calcul de Eq.10.5 en deux temps:

on intègre sur $r$ :

$$I_{1}(\theta )=\Gamma _{PP}(d)=\int _{-\infty }^{\infty }h(r_{1}+r)h(r_{1}+r+d)dr$$ (9.6)

Puis on intègre le résultat suivant $\theta$ :

$$I_{2}=\int _{0}^{\theta }I_{1}(\theta )d\theta$$ (9.7)

9.3.2.4.1 Calcul de $I_{1}$.

$I_{1}(\theta )$ apparaît donc comme la fonction d'autocorrélation de la réponse impulsionnelle $h$ à la distance $d$. ^9.5

$$I_{1}(\theta ) = \frac{1}{2\pi \sigma ^{2}}\int _{-\infty }^{\infty }e^{-\frac{r^{2}}{2\sigma ^{2}}}e^{-\frac{(r-d)^{2}}{2\sigma ^{2}}}dr$$

$$= \frac{1}{2\pi \sigma ^{2}}e^{-\frac{d^{2}}{4\sigma ^{2}}}\int _{-\infty }^{\infty }e^{-\frac{(r-d/2)^{2}}{\sigma ^{2}}}dr$$

$$= \frac{1}{2\sigma \sqrt{\pi }}e^{-\frac{d^{2}}{4\sigma ^{2}}}$$ (9.8)

9.3.2.4.2 Calcul de $I_{2}$.

^9.6

Pour l'intégration de (10.5) suivant $\theta$, il est nécessaire de définir explicitement $d(\theta )$ en fonction des écarts $d_{x}$ et $d_{y}$ séparant les deux pixels considérés.

Figure 10.10: Calcul de $d$

Avec les notations explicitées Fig.10.10, on obtient simplement:

$$d(\theta )=l_{2}-l_{1}=\cos (\theta )d_{y}-\sin (\theta )d_{x}$$

On distingue 2 cas suivant la valeur de $d_{x}$.

9.3.2.4.2.1 Cas où $d_{x}\neq 0\protect$:

On pose alors $\tan (\psi )=\frac{d_{y}}{d_{x}}$ qui nous permet de réécrire la distance $d(\theta )$ comme:

$$d(\theta )=d_{x}(\tan (\psi )\cos (\theta )-\sin (\theta ))=\frac{d_{x}}{\cos (\psi )}\sin (\psi -\theta )$$ (9.9)

et son carré comme:

$$d^{2}(\theta )={\left[ \frac{d_{x}}{\cos (\psi )}\sin (\psi -\the... ...{2}=-\frac{d_{x}^{2}}{2\cos ^{2}(\psi )}\left[ \cos (2(\psi -\theta ))-1\right]$$ (9.10)

De ce fait en remplaçant $d^{2}$ par sa valeur dans Eq.10.8 et utilisant Eq.10.7, nous obtenons pour $I_{2}$ en fonction des écarts $d_{x}$ et $d_{y}$:

$$I_{2}(d_{x},d_{y})=\frac{e^{K_{1}}}{\sigma \sqrt{2\pi }}\int _{0}^{\pi }e^{-K_{1}\cos (2(\theta -\psi ))}d\theta$$ (9.11)

avec $K_{1}=-\frac{d_{x}^{2}}{8\sigma ^{2}\cos ^{2}(\arctan (\frac{d_{y}}{d_{x}}))}$

En rappelant que la fonction modifiée de Bessel de premier ordre $I_{0}(x)$ est telle que:

$$I_{0}(x)=\frac{1}{\pi }\int _{0}^{\pi }e^{\pm x\cos (\theta )}d\theta$$

On trouve finalement que :

$$I_{2}(d_{x},d_{y})=\frac{\sqrt{\pi }e^{K_{1}}}{2\sigma }I_{0}(K_{1})$$ (9.12)

9.3.2.4.2.2 Cas où $d_{x}=0$:

Un calcul analogue à ce qui vient d'être fait montre que

$$I_{2}(0,d_{y})=\frac{\sqrt{\pi }e^{K_{2}}}{2\sigma }I_{0}(K_{2})$$ (9.13)

avec $K_{2}=-\frac{d_{y}^{2}}{8\sigma ^{2}}$

La fonction $I_{2}$ peut être prolongée par continuité puisque :

$$\lim _{d_{x}\rightarrow 0}K_{1}=K_{2}$$

On note par $S$ la surface décrite par $I_{2}(d_{x},d_{y})$ lorsqu'on fait varier les écarts $d_{x}$ et $d_{y}$ (Fig.10.11). Pour chaque couple de composantes $n_{1}$ et $n_{2}$, nous obtenons une valeur correspondante pour les écarts $d_{x}$ et $d_{y}$. De ce fait, la valeur de $\{H^{t}H\}_{n_{1},n_{2}}$ se lit directement sur la surface $S$ aux coordonnées $(d_{x},d_{y})$ correspondantes.

Figure: Représentation de la surface $S$ correspondant à l'interprétation géométrique de $H^{t}H_{n_{2},n_{1}}$.

9.3.2.5 Construction pratique de $\mathbf{H}^{t}\mathbf{H}$.

Pour construire la matrice $\mathbf{H}^{t}\mathbf{H}$ partant de $I_{2}(d_{x},d_{y})$, il n'est pas nécessaire de conserver toutes les valeurs de $(H^{t}H)_{n_{2},n_{1}}$pour les différents couples $(n_{1},n_{2})\in [1,N]\times [1,N]$ possibles dans l'image à reconstruire. En effet, pour construire la valeur de $(H^{t}H)_{n_{2},n_{1}}$ pour un couple $(n_{1},n_{2})$ particulier, on peut utiliser un tableau $HtHTab(i,j)$ à deux dimensions. $i\in [-N_{x},N_{x}]$ caractérise les écarts possibles entre pixels suivant la direction $x$ pour l'image envisagée et $j\in [-N_{y},N_{y}]$ ceux suivant $y$. En effet, les déplacements sur l'image sont quantifiés par la taille du pixel $\Delta x$ et $\Delta y$ conduisant à $d_{x}=i\times \Delta x$ et $d_{y}=j\times \Delta y$. On remplit le tableau $H^{t}HTab$ en utilisant Eq.10.12 et Eq.10.13. Autrement dit $HtHTab(i,j)=I_{2}(d_{x}=i.\Delta x,d_{y}=j.\Delta y)$. Pour les indices $n_{1}$ et $n_{2}$ dans l'image tel que $n_{1}=j_{1}+N_{x}\times (i_{1}-1)$ et $n_{2}=j_{2}+N_{x}\times i_{2}$. On obtient la valeur de $(H^{t}H)_{n_{2},n_{1}}$ par $HtHTab(i_{2}-i_{1},j_{2}-j_{1})$. On peut donc ainsi de manière très simple et très rapide recalculer n'importe quelle ligne où colonne de la matrice produit $\mathbf{H}^{t}\mathbf{H}$ (Voir Fig.10.12). De plus, on diminue la taille de la matrice $\mathbf{H}^{t}\mathbf{H}$ de manière importante. En effet, pour une image ECAT HR+ classique, $N_{x}=N_{y}=128$. La taille globale de $\mathbf{H}^{t}\mathbf{H}$ serait normalement $[16384\times 16384]$, ici elle n'est plus que de $[256\times 256]$ soit $4096$ fois plus petite. De plus, on s'affranchit du produit matriciel $\mathbf{H}^{t}\mathbf{H}$. Pour des raisons de symétrie de révolution de la fonction $I_{2}$, on peut encore diminuer la taille du tableau $HtHTab$ par 4 en travaillant sur les valeurs absolues des écart $d_{x}$ et $d_{y}$.

Figure: Construction de $H^{t}H_{n_{2},n_{1}}$ à partir de $S$.

On obtient alors les algorithmes Alg.10

pour la construction du $\mathbf{H}^{t}\mathbf{H}$ et Alg.11

pour le produit matriciel partant de cette matrice.