




Next: 11. Conclusion et Perspectives.
Up: 10. Evaluation.
Previous: 10.2 Evaluation des reconstructions
Contents
Index
Subsections
Afin de montrer l'intérêt de la simulation sur la détermination des caractéristiques
du bruit dans les images après reconstruction, nous allons chercher à estimer
la variance en chaque pixel sur un fantôme particulier. Il est clair que ce
genre d'étude ne peut être mené par la réalisation d'une série de mesures car
elle impliquerait un trop grand nombre d'acquisitions.
Le fantôme envisagé est un cylindre homogène de rayon 186 mm situé au centre
du champ de vue. Le cylindre en question couvre l'intégralité du tunnel imagé
suivant la direction  . L'avantage de ce fantôme est son homogénéité
et sa symétrie de révolution qui ne génère pas d'aberrations liées à la géométrie
de l'objet émetteur. On peut ainsi totalement voir les instationnarités liés
au processus d'acquisition/reconstruction.
. L'avantage de ce fantôme est son homogénéité
et sa symétrie de révolution qui ne génère pas d'aberrations liées à la géométrie
de l'objet émetteur. On peut ainsi totalement voir les instationnarités liés
au processus d'acquisition/reconstruction.
Partant de ce fantôme, nous allons générer un sinogramme non bruité complet.
Ce sinogramme est reconstruit suivant une méthode standard par rétroprojection
des données filtrées d'une part et par un méthode algébrique de reconstruction
par gradient conjugué (on utilise uniquement le premier segment ). Ces deux
reconstructions nous fournissent deux volumes de référence
 pour la reconstruction standard et
pour la reconstruction standard et
 pour la reconstruction
algébrique. Les reconstructions de sinogrammes bruités faites ultérieurement
seront comparées à ces volumes.
pour la reconstruction
algébrique. Les reconstructions de sinogrammes bruités faites ultérieurement
seront comparées à ces volumes.
Nous allons maintenant simuler 50 acquisitions. Pour chaque simulation, nous
envisageons différentes reconstructions dans le but d'obtenir une image de variance
pour chaque type. La démarche est la suivante:
- Création d'un sinogramme bruité par l'utilisation de notre modèle de bruit.
La valeur moyenne sur le fantôme étant la même que dans le cas du fantôme numérique
d'Hoffman, nous utilisons les constantes
 et
et
 afin de simuler une acquisition présentant 100M de coups (cf.
Tab.6.7 du Ch.6).
afin de simuler une acquisition présentant 100M de coups (cf.
Tab.6.7 du Ch.6).
- Reconstruction du premier segment pour l'estimation par projection des vues
manquantes.
- Reconstruction du sinogramme complet par FBP3D (
 ,
,
 ), FORE+FBP (
), FORE+FBP (
 ), FORE+GC
(
), FORE+GC
(
 ), FOSA+FBP (
), FOSA+FBP (
 ), FOSA+GC
(
), FOSA+GC
(
 ).
).
- Mise à jour de l'image de variance pour l'itération considérée. Retour à 1.
Nous donnons Fig.11.15 l'illustration des résultats pour un
plan transaxial situé au centre du champ de vue. Pour ce plan, nous donnons
également les profils passant par le centre suivant les directions associées
à  et
et  .
.
D'une manière générale, nous voyons que la variance pour ces deux modes de reconstruction
est du même ordre de grandeur (Fig.11.13).
Figure 11.13:
Comparaison de la variance dans un plan transaxial pour des reconstructions de type FBP3D etRebinning+FBP. Les profils illustrés correspondent à la moyenne des deux profils passant par le centre du champ de vue (Un suivant la direction  et l'autre suivant la direction
et l'autre suivant la direction  .
.
|
|
En revanche, nous voyons nettement que la variance pour les reconstructions
impliquant une méthode de rebinning montrent une plus grande instationnarité.
La variance est plus élevée au centre du champ de vue et diminue à mesure que
l'on s'éloigne du centre. Ce phénomène semble plus accentué pour l'algorithme
de rebinning FOSA.
Il apparaît nettement que la variance des voxels pour une reconstruction algébrique
est plus faible que dans le cas d'une reconstruction standard.11.14
Figure 11.14:
Comparaison de la variance dans un plan transaxial pour des reconstructions de type FBP3D etRebinning+GC. Les profils illustrés correspondent à la moyenne des deux profils passant par le centre du champ de vue (Un suivant la direction  et l'autre suivant la direction
et l'autre suivant la direction  .
.
|
|
Cela est particulièrement vrai pour les voxels situés à l'intérieur du cylindre.
Dans le cas précis d'un fantôme présentant une grande région homogène, la méthode
de reconstruction algébrique est optimale. Nous aurions même pu augmenter la
constante de lissage et donc diminuer encore la variance à l'intérieur du cylindre.
Il faut également remarquer la forte variation de la variance sur les bords
du cylindre. La reconstruction algébrique ne lisse pas de manière uniforme,
il y aura donc a proximité des discontinuités des variances locales plus élevées.
Toutefois, vue la forte différence de valeurs de la variance entre les voxels
proches des discontinuités et ceux situés à l'intérieur du cylindre, il me semble
que ces valeurs sont également le reflet d'un biais systématique entre la reconstruction
et le fantôme
 servant de référence (notamment du fait du filtrage
effectué sur le volume juste avant projection lors de la création d'un sinogramme
de bruit).
servant de référence (notamment du fait du filtrage
effectué sur le volume juste avant projection lors de la création d'un sinogramme
de bruit).
![\begin{landscape}
% latex2html id marker 19865\begin{figure}[htbp]
\centering\...
...u de bruit relatif à 260M de coups (50 itérations).
}\end{figure}\end{landscape}](img1498.png)
Nous venons de voir qu'il existait déjà une instationnarité sur la variance
des voxels dans un plan. Nous avons, en introduction de cette thèse, énoncé
le fait que l'instationnarité du bruit sur les images était un handicap dans
les études d'activation. Une grosse partie du travail de MJ. Antoine durant
sa thèse a consisté à montrer l'influence de ces instationnarités sur la détection.
Dans ce paragraphe, nous nous intéressons à l'influence de la corrélation inhérente
aux images TEP. Rappelons brièvement que l'autocorrélation peut être reliée,
sous l'hypothèse de champ gaussien, à un paramètre 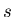 , appelé smoothness.
On montre, en 2D, que
, appelé smoothness.
On montre, en 2D, que  peut être estimé à partir de la variance
des dérivées premières de l'image suivant les directions
peut être estimé à partir de la variance
des dérivées premières de l'image suivant les directions  et
et  .
Ce paramètre correspond à l'écart-type qu'il faut choisir pour un noyau gaussien
bidimensionnel, de manière à ce que le filtrage d'un bruit blanc par ce noyau
conduise à la même valeur moyenne de corrélation que celle observée. Nous allons
nous intéresser ici uniquement à l'instationnarité suivant un axe longitudinal
(suivant
.
Ce paramètre correspond à l'écart-type qu'il faut choisir pour un noyau gaussien
bidimensionnel, de manière à ce que le filtrage d'un bruit blanc par ce noyau
conduise à la même valeur moyenne de corrélation que celle observée. Nous allons
nous intéresser ici uniquement à l'instationnarité suivant un axe longitudinal
(suivant  ). Fig.11.16 nous donnons la variation
du paramètre
). Fig.11.16 nous donnons la variation
du paramètre  observé (a) et simulé (b).
observé (a) et simulé (b).
Figure:
Valeur du paramètre
 suivant la direction
suivant la direction  pour la caméra ECAT HR+(d'après [4])
pour la caméra ECAT HR+(d'après [4])
[Mesuré sur acquisition.]
![\resizebox*{0,45\textwidth}{!}{\psfrag{Wxy}[][][2]{\( \sqrt{2}.s_{xy} \)}\includegraphics{imgps/w_MJ_annote.eps}}](img1500.png) [Calculé avec notre modèle de bruit.]
![\resizebox*{0,45\textwidth}{!}{\psfrag{Wxy}[][][2]{\( \sqrt{2}.s_{xy} \)}\includegraphics{crayps/cylps/Wxy_2d_FBP3D_calc.ps}}](img1501.png)
|
Nous montrons ainsi que notre chaîne de projection/reconstruction permet de
retrouver l'instationnarité observé par Antoine sur la caméra ECAT HR+. Cette
instationnarité provient essentiellement du processus de reprojection pour estimer
les vues manquantes. C'est pourquoi dans un deuxième temps, nous avons cherché
à voir comment le rebinning modifiait cette instationnarité. Nous donnons
donc Fig.11.17, la variation longitudinale  pour les 3 reconstructions FORE+FBP, FOSA+FBP et FBP3D. Nous constatons que
les reconstructions post-rebinning, et notamment l'algorithme FORE, atténuent
la valeur de la corrélation (
pour les 3 reconstructions FORE+FBP, FOSA+FBP et FBP3D. Nous constatons que
les reconstructions post-rebinning, et notamment l'algorithme FORE, atténuent
la valeur de la corrélation ( est plus faible) pour les plans situés
aux extrémités du cylindre.
est plus faible) pour les plans situés
aux extrémités du cylindre.
Figure:
Valeur du paramètre
 suivant la direction
suivant la direction  pour différents types de reconstruction provenant d'un sinogramme simulé.
pour différents types de reconstruction provenant d'un sinogramme simulé.
|
|





Next: 11. Conclusion et Perspectives.
Up: 10. Evaluation.
Previous: 10.2 Evaluation des reconstructions
Contents
Index
Lecomte Jean François
2002-09-07
![]() . L'avantage de ce fantôme est son homogénéité
et sa symétrie de révolution qui ne génère pas d'aberrations liées à la géométrie
de l'objet émetteur. On peut ainsi totalement voir les instationnarités liés
au processus d'acquisition/reconstruction.
. L'avantage de ce fantôme est son homogénéité
et sa symétrie de révolution qui ne génère pas d'aberrations liées à la géométrie
de l'objet émetteur. On peut ainsi totalement voir les instationnarités liés
au processus d'acquisition/reconstruction.
![]() pour la reconstruction standard et
pour la reconstruction standard et
![]() pour la reconstruction
algébrique. Les reconstructions de sinogrammes bruités faites ultérieurement
seront comparées à ces volumes.
pour la reconstruction
algébrique. Les reconstructions de sinogrammes bruités faites ultérieurement
seront comparées à ces volumes.
![]() et
et ![]() .
.


![]() , appelé smoothness.
On montre, en 2D, que
, appelé smoothness.
On montre, en 2D, que ![]() peut être estimé à partir de la variance
des dérivées premières de l'image suivant les directions
peut être estimé à partir de la variance
des dérivées premières de l'image suivant les directions ![]() et
et ![]() .
Ce paramètre correspond à l'écart-type qu'il faut choisir pour un noyau gaussien
bidimensionnel, de manière à ce que le filtrage d'un bruit blanc par ce noyau
conduise à la même valeur moyenne de corrélation que celle observée. Nous allons
nous intéresser ici uniquement à l'instationnarité suivant un axe longitudinal
(suivant
.
Ce paramètre correspond à l'écart-type qu'il faut choisir pour un noyau gaussien
bidimensionnel, de manière à ce que le filtrage d'un bruit blanc par ce noyau
conduise à la même valeur moyenne de corrélation que celle observée. Nous allons
nous intéresser ici uniquement à l'instationnarité suivant un axe longitudinal
(suivant ![]() ). Fig.11.16 nous donnons la variation
du paramètre
). Fig.11.16 nous donnons la variation
du paramètre ![]() observé (a) et simulé (b).
observé (a) et simulé (b).
![\resizebox*{0,45\textwidth}{!}{\psfrag{Wxy}[][][2]{\( \sqrt{2}.s_{xy} \)}\includegraphics{imgps/w_MJ_annote.eps}}](img1500.png) [Calculé avec notre modèle de bruit.]
[Calculé avec notre modèle de bruit.]
![\resizebox*{0,45\textwidth}{!}{\psfrag{Wxy}[][][2]{\( \sqrt{2}.s_{xy} \)}\includegraphics{crayps/cylps/Wxy_2d_FBP3D_calc.ps}}](img1501.png)
