




Next: C. Discrétisation d'un Volume.
Up: B. L'algorithme OSEM-OSL et
Previous: B.1 Modèle Poissonien [97]
Contents
Index
Subsections
L'émission étant un phénomène statistique, trouver un algorithme itératif qui
intègre cette information dans sa résolution ne pouvait que séduire. C'est le
cas de l'algorithme EM (pour Expectation Maximisation) [31,55].
Cet algorithme est de loin le plus connu et le plus utilisé des algorithmes
itératifs de reconstruction.
Nous avons vu qu'en reconstruction et dans le cas d'une modélisation poissonienne
et dans le cadre d'une régularisation markovienne, le critère du MAP que nous
devions minimiser s'écrivait:
La constante  , que nous rajoutons, nous permet de controler le
poids de la régularisation (
, que nous rajoutons, nous permet de controler le
poids de la régularisation ( ) vis à vis de l'importance accordée
aux données (
) vis à vis de l'importance accordée
aux données ( ). La plupart du temps, on introduit à ce niveau une
variable auxiliaire non-observée
). La plupart du temps, on introduit à ce niveau une
variable auxiliaire non-observée  , les données complètes représentant
le nombre de photons émis par le voxel
, les données complètes représentant
le nombre de photons émis par le voxel  et captés par le détecteur référencé
par
et captés par le détecteur référencé
par 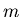 . Nous avons alors le nombre de coups détectés par un capteur qui
s'écrit comme:
L'algorithme consiste alors en deux phases: l'estimation des
. Nous avons alors le nombre de coups détectés par un capteur qui
s'écrit comme:
L'algorithme consiste alors en deux phases: l'estimation des  (Expectation)
et la maximisation de
(Expectation)
et la maximisation de
 (Maximisation). En combinant
les deux étapes, on arrive à une expression [41]:
(Maximisation). En combinant
les deux étapes, on arrive à une expression [41]:
où
 . Evidemment dans cette
expression, le terme
. Evidemment dans cette
expression, le terme
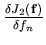 qui représente
la dérivée locale de notre information a priori, nous pose problème (cf
Par.9.2.4.5). Green propose, à l'itération
qui représente
la dérivée locale de notre information a priori, nous pose problème (cf
Par.9.2.4.5). Green propose, à l'itération 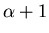 ,
de calculer ce terme en partant de l'estimée à l'itération
,
de calculer ce terme en partant de l'estimée à l'itération  (d'où
le nom de l'algorithme OSL pour One Step Late). Nous avons alors, en utilisant
l'expression de la dérivée locale (Eq.9.5):
(d'où
le nom de l'algorithme OSL pour One Step Late). Nous avons alors, en utilisant
l'expression de la dérivée locale (Eq.9.5):
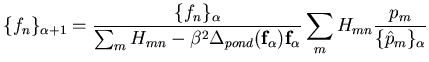 |
(B.1) |
En l'état, l'implémentation de cette expression conduit à l'algorithme EM-OSL.
Un inconvénient quant à l'utilisation de cet algorithme est la lenteur de la
convergence. C'est pourquoi, dans un souci d'accélérer cette convergence nous
utiliserons la technique Ordered Subset (OS), qui conduit à l'algorithme
que nous avons implémenté OSEM-OSL.
La technique OS comprend deux concepts qui permettent l'accélération: le réarrangement
des projections (Ordered) et leur partitionnement (Subset)
Ce réarrangement peut se comprendre de manière intuitive. Notre sinogramme correspond
à un ensemble de plan  tournant autour de l'objet à imager. Le nombre
de vue
tournant autour de l'objet à imager. Le nombre
de vue
 est grand (144), autrement dit la différence angulaire
entre deux plans succesifs (2
est grand (144), autrement dit la différence angulaire
entre deux plans succesifs (2  successif) est faible (1.25
successif) est faible (1.25 ).
Il va sans dire que les informations apportées par chacun de ces deux plans
sur l'image
).
Il va sans dire que les informations apportées par chacun de ces deux plans
sur l'image
 sont proches. Il en va tout autrement, si entre deux
itérations successives, les angles de vue sont éloignés (grande différence angulaire).
Si donc, on veut accroitre la vitesse de convergence de l'algorithme, il faut
fournir d'une itération à l'autre une information qui soit la plus différente
possible de celle qu'il vient de recevoir. Intuitivement, on se dit qu'un écart
angulaire
sont proches. Il en va tout autrement, si entre deux
itérations successives, les angles de vue sont éloignés (grande différence angulaire).
Si donc, on veut accroitre la vitesse de convergence de l'algorithme, il faut
fournir d'une itération à l'autre une information qui soit la plus différente
possible de celle qu'il vient de recevoir. Intuitivement, on se dit qu'un écart
angulaire

 serait
optimal. Nous envisageons le réarrangement tel qu'il est décrit par Herman [43].
Supposons que nous ayons 10 directions de projections, plutôt que de parcourir
les projections dans l'ordre 1,2,3,... nous les parcourons de sorte d'avoir
toujours le plus grand écart angulaire (Tab.B.1).
serait
optimal. Nous envisageons le réarrangement tel qu'il est décrit par Herman [43].
Supposons que nous ayons 10 directions de projections, plutôt que de parcourir
les projections dans l'ordre 1,2,3,... nous les parcourons de sorte d'avoir
toujours le plus grand écart angulaire (Tab.B.1).
Toujours en travaillant sur les redondances liées au différentes vues, on peut
se poser la question de savoir ce que donnerait la reconstruction en sous échantillonant
le sinogramme (Ne prendre qu'un angle de vue tous les 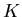 ). On crée un
sous ensemble du sinogramme (subset). Avec un sinogramme on peut évidemment
construire
). On crée un
sous ensemble du sinogramme (subset). Avec un sinogramme on peut évidemment
construire 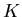 subsets.
subsets.
Partant de cette subdivision, on va reconstruire le volume pour un subset. L'image
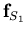 obtenue sert de point de départ pour une reconstruction
sur le deuxième subset, et ainsi de suite. Le passage sur tous les subsets va
constituer une itération (un passage de toutes les projections), que l'on répète
jusqu'à convergence. En parcourant les subsets dans l'ordre, on obtient juste
une technique de réarrangement qui consiste à prendre les projections dans l'ordre
obtenue sert de point de départ pour une reconstruction
sur le deuxième subset, et ainsi de suite. Le passage sur tous les subsets va
constituer une itération (un passage de toutes les projections), que l'on répète
jusqu'à convergence. En parcourant les subsets dans l'ordre, on obtient juste
une technique de réarrangement qui consiste à prendre les projections dans l'ordre
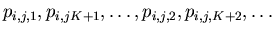 . En revanche,
on peut combiner les deux approches en définissant un ordre de parcours des
subsets. De sorte que l'information apportée par deux subsets successifs soit
la plus différente possible. Cette approche définit l'algorithme Ordered Subset
(Alg.13)
. En revanche,
on peut combiner les deux approches en définissant un ordre de parcours des
subsets. De sorte que l'information apportée par deux subsets successifs soit
la plus différente possible. Cette approche définit l'algorithme Ordered Subset
(Alg.13)






Next: C. Discrétisation d'un Volume.
Up: B. L'algorithme OSEM-OSL et
Previous: B.1 Modèle Poissonien [97]
Contents
Index
Lecomte Jean François
2002-09-07
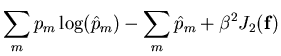
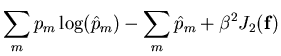
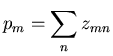
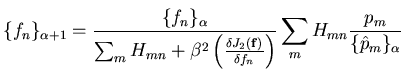
![]() tournant autour de l'objet à imager. Le nombre
de vue
tournant autour de l'objet à imager. Le nombre
de vue
![]() est grand (144), autrement dit la différence angulaire
entre deux plans succesifs (2
est grand (144), autrement dit la différence angulaire
entre deux plans succesifs (2 ![]() successif) est faible (1.25
successif) est faible (1.25![]() ).
Il va sans dire que les informations apportées par chacun de ces deux plans
sur l'image
).
Il va sans dire que les informations apportées par chacun de ces deux plans
sur l'image
![]() sont proches. Il en va tout autrement, si entre deux
itérations successives, les angles de vue sont éloignés (grande différence angulaire).
Si donc, on veut accroitre la vitesse de convergence de l'algorithme, il faut
fournir d'une itération à l'autre une information qui soit la plus différente
possible de celle qu'il vient de recevoir. Intuitivement, on se dit qu'un écart
angulaire
sont proches. Il en va tout autrement, si entre deux
itérations successives, les angles de vue sont éloignés (grande différence angulaire).
Si donc, on veut accroitre la vitesse de convergence de l'algorithme, il faut
fournir d'une itération à l'autre une information qui soit la plus différente
possible de celle qu'il vient de recevoir. Intuitivement, on se dit qu'un écart
angulaire
![]()
![]() serait
optimal. Nous envisageons le réarrangement tel qu'il est décrit par Herman [43].
Supposons que nous ayons 10 directions de projections, plutôt que de parcourir
les projections dans l'ordre 1,2,3,... nous les parcourons de sorte d'avoir
toujours le plus grand écart angulaire (Tab.B.1).
serait
optimal. Nous envisageons le réarrangement tel qu'il est décrit par Herman [43].
Supposons que nous ayons 10 directions de projections, plutôt que de parcourir
les projections dans l'ordre 1,2,3,... nous les parcourons de sorte d'avoir
toujours le plus grand écart angulaire (Tab.B.1).
![]() ). On crée un
sous ensemble du sinogramme (subset). Avec un sinogramme on peut évidemment
construire
). On crée un
sous ensemble du sinogramme (subset). Avec un sinogramme on peut évidemment
construire ![]() subsets.
subsets.
