Nous venons de définir un modèle de bruit que nous appliquons à tout volume
numérique pour simuler l'acquisition d'un sinogramme. Nous avons ensuite estimé
les valeurs des constantes qui contrôlent le modèle pour différents niveaux
de bruit. Notre souci était d'obtenir des sinogrammes de bruit présentant une
distribution analogue à celle obtenue partant de sinogrammes réels. Il s'agit
maintenant de vérifier que les sinogrammes obtenus, après reconstruction, conduisent
à des images analogues à celle provenant de sinogrammes réels. Nous repartons
donc de notre fantôme numérique recalé. Nous cherchons à construire un sinogramme
![]() présentant les mêmes caractéristiques statistiques que le sinogramme
réel
présentant les mêmes caractéristiques statistiques que le sinogramme
réel ![]() . Nous obtenons alors deux constantes qui sont
. Nous obtenons alors deux constantes qui sont
![]() et
et ![]() . Nous effectuons, en chaque voxel du fantôme numérique,
un tirage aléatoire suivant la loi Eq.6.2 pour obtenir une valeur
de bruit
. Nous effectuons, en chaque voxel du fantôme numérique,
un tirage aléatoire suivant la loi Eq.6.2 pour obtenir une valeur
de bruit
![]() . Nous construisons un fantôme bruité
. Nous construisons un fantôme bruité
![]() .
Nous projetons ce fantôme pour obtenir un sinogramme bruité. Afin d'estimer
les vues manquantes de ce sinogramme, nous le reconstruisons en utilisant uniquement
le premier segment et en effectuant une reconstruction 2D par plan (cf Ch.7).
Cette reconstruction est ensuite reprojetée analytiquement afin d'obtenir l'information
pour les éléments qui ne sont pas vus du fait de la géométrie cylindrique d'acquisition.
Nous pouvons alors reconstruire le sinogramme ainsi complété par une méthode
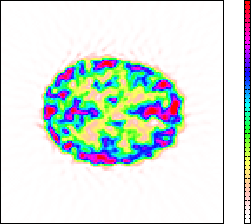
standard. Une représentation de cette reconstruction pour un plan de coupe transaxial
est donnée Fig.6.25.a.
.
Nous projetons ce fantôme pour obtenir un sinogramme bruité. Afin d'estimer
les vues manquantes de ce sinogramme, nous le reconstruisons en utilisant uniquement
le premier segment et en effectuant une reconstruction 2D par plan (cf Ch.7).
Cette reconstruction est ensuite reprojetée analytiquement afin d'obtenir l'information
pour les éléments qui ne sont pas vus du fait de la géométrie cylindrique d'acquisition.
Nous pouvons alors reconstruire le sinogramme ainsi complété par une méthode
standard. Une représentation de cette reconstruction pour un plan de coupe transaxial
est donnée Fig.6.25.a.
|

|
| [Simulation] | [Réel] |
Malheureusement pour nous, ce n'est pas parceque deux distributions ont la même moyenne et la même variance qu'elles sont identiques. Est ce à dire qu'il nous faut rejeter notre modèle ?
L'étude qui précède nous a permis de rendre les puissances des bruits calculées
et réelles équivalentes. Toutefois, cela nous a conduit à des constantes ![]() .
Ce qui veut dire, que l'écart type
.
Ce qui veut dire, que l'écart type
![]() du bruit
que nous ajoutons sur notre volume peut devenir plus important que le signal
lui même
du bruit
que nous ajoutons sur notre volume peut devenir plus important que le signal
lui même
![]() . Autrement dit, le bruit dans le volume
. Autrement dit, le bruit dans le volume ![]() juste avant la projection détruit quasi-totalement l'information spatiale relative
au signal. Il faut donc trouver un moyen de conserver une information spatiale
dans ce volume
juste avant la projection détruit quasi-totalement l'information spatiale relative
au signal. Il faut donc trouver un moyen de conserver une information spatiale
dans ce volume ![]() . L'idée que nous proposons est donc de construire
différemment la distribution de bruit
. L'idée que nous proposons est donc de construire
différemment la distribution de bruit ![]() en ne réalisant un tirage
aléatoire que sur un sous ensemble des
en ne réalisant un tirage
aléatoire que sur un sous ensemble des ![]() voxels du fantôme numérique.
voxels du fantôme numérique.
Imaginons en 2D une partie de notre image (3x3=9 voxels de ![]() à
à ![]() ).
On considère également que chaque pixel est la réalisation d'un processus aléatoire
).
On considère également que chaque pixel est la réalisation d'un processus aléatoire
![]() . Chacun de ces processus peut se mettre sous la forme
. Chacun de ces processus peut se mettre sous la forme
![]() , où
, où ![]() représente la valeur déterministe
de la distribution radioactive et
représente la valeur déterministe
de la distribution radioactive et ![]() son aspect aléatoire, son bruit.
On suppose pour simplifier que ce bruit est gaussien de variance
son aspect aléatoire, son bruit.
On suppose pour simplifier que ce bruit est gaussien de variance
![]() .
La projection envisagée Fig.6.26.a revient à construire une
variable aléatoire
.
La projection envisagée Fig.6.26.a revient à construire une
variable aléatoire
![]()
| [Projection sans sous-échantillonnage.] | [Projection avec sous-échantillonnage.] |
|

|
Supposons maintenant que sur ces 9 pixels, un seul des pixel soit la réalisation
d'un processus aléatoire {![]() par exemple) et qu'il se mette sous
la forme
par exemple) et qu'il se mette sous
la forme
![]() . La projection devient un processus aléatoire
défini par
. La projection devient un processus aléatoire
défini par
![]() (Fig.6.26.b). Son espérance
est alors
(Fig.6.26.b). Son espérance
est alors
![]() et sa variance
et sa variance
![]() .
Pour que les variances soient équivalentes dans les deux cas, il suffit de prendre
.
Pour que les variances soient équivalentes dans les deux cas, il suffit de prendre
![]() . Si on suppose que l'image est
suffisamment lisse pour que les variations entre pixels soit telles que
. Si on suppose que l'image est
suffisamment lisse pour que les variations entre pixels soit telles que
![]() où
où ![]() représente la moyenne sur les neufs pixels, alors le fait
de ne bruiter qu'un voxel sur les neufs, nous permet de construire des projections
pour lesquelles le bruit est équivalent (en terme de moyenne et de variance)
au bruit que nous aurions obtenu en bruitant les neufs pixels.
représente la moyenne sur les neufs pixels, alors le fait
de ne bruiter qu'un voxel sur les neufs, nous permet de construire des projections
pour lesquelles le bruit est équivalent (en terme de moyenne et de variance)
au bruit que nous aurions obtenu en bruitant les neufs pixels.
Ainsi, pour bruiter notre image, nous envisageons la procédure suivante.
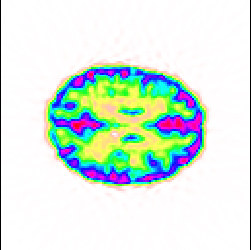
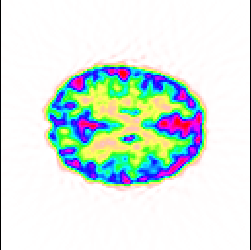
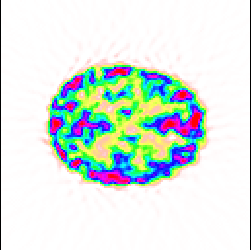
Nous donnons Fig.6.27 les images issues de ces volumes émetteurs pour différentes valeurs de sous échantillonnage.
| [
|
[
|

|
|
|
[
|
[
|
|
|
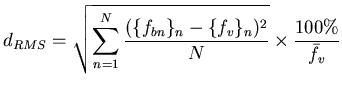
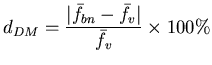
|
|
Intensité du voxel d'indice |
|
|
Intensité du voxel d'indice |
|
|
Valeur moyenne sur le volume (sinogramme simulé). |
|
|
Valeur moyenne sur le volume (sinogramme réel). |
| Nombre de voxels dans le volume. |
Ces critères standards [60,42] sont utilisés comme définis par
Ouyang dans [72]. Pour différentes valeurs du sous-échantillonnage
![]() , nous allons calculer les valeurs de ces deux critères. Les résultats
obtenus sont illustrés sous forme de courbes Fig.6.28.
, nous allons calculer les valeurs de ces deux critères. Les résultats
obtenus sont illustrés sous forme de courbes Fig.6.28.